题目内容
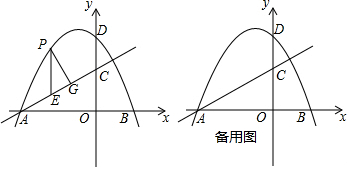
5.在四边形ABCD中,AC⊥BD于点O,AC=6,四边形ABCD的面积为24.(1)如图1,求BD的长;
(2)如图2,若AD=5,AD∥BC,求证:四边形ABCD是菱形.

分析 (1)由AC⊥BD,推出S四边形ABCD=S△ABD+S△CBD=$\frac{1}{2}$BD•AO$+\frac{1}{2}$BD•OC=$\frac{1}{2}$BD(AO+OC)=$\frac{1}{2}$BD×6=24,由此即可解决问题;
(2)设OA=x,OD=y,则OB=8-y,OC=6-x,想办法构建方程组即可解决问题;
解答 解:(1)∵AC⊥BD,
∴S四边形ABCD=S△ABD+S△CBD=$\frac{1}{2}$BD•AO$+\frac{1}{2}$BD•OC=$\frac{1}{2}$BD(AO+OC)=$\frac{1}{2}$BD×6=24,
∴BD=8;
(2)设OA=x,OD=y,则OB=8-y,OC=6-x,
∵AD∥BC,
∴$\frac{OA}{OC}$=$\frac{OD}{OB}$,
∴$\frac{x}{6-x}$=$\frac{y}{8-y}$,
∴4x=3y,
∵x2+y2=25,x>0,y>0,
∴x=3,y=4,
∴OA=OC,OB=OD,
∴四边形ABCD是平行四边形,
∵AC⊥BD,
∴四边形ABCD是菱形.
点评 本题考查菱形的判定、平行四边形的判定和性质,平行线分线段成比例定理、二元一次方程组等知识,解题的关键是学会构建方程组解决问题,属于中考常考题型,体现了数形结合的思想.

练习册系列答案
 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案
相关题目
14.已知实数x>0,实数y满足式子y=3-$\sqrt{{x}^{2}-2}+\sqrt{2-{x}^{2}}$,则x2y=( )
| A. | 0 | B. | 3 | C. | 6 | D. | 3$\sqrt{2}$ |
 如图,已知A(m,3)是一次函数y=kx+b与反函数y=$\frac{6}{x}$(x>0)的交点.
如图,已知A(m,3)是一次函数y=kx+b与反函数y=$\frac{6}{x}$(x>0)的交点.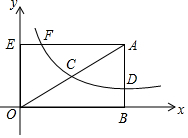 如图,矩形ABOE的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.
如图,矩形ABOE的顶点O在坐标原点,点B在x轴上,∠ABO=90°,∠AOB=30°,OB=2$\sqrt{3}$,反比例函数y=$\frac{k}{x}$(x>0)的图象经过OA的中点C,交AB于点D.