题目内容
3. 如图,已知在△ABC中,∠B与∠C的平分线交于点P,∠BPC=125°时,则∠A=70°.
如图,已知在△ABC中,∠B与∠C的平分线交于点P,∠BPC=125°时,则∠A=70°.
分析 根据三角形的内角和等于180°,求出∠PBC+∠PCB的度数,所以∠ABC+∠ACB可以求出.在△ABC中,根据三角形内角和定理即可求出∠A的度数.
解答 解:在△PBC中,∵∠BPC=125°,
∴∠PBC+∠PCB=180°-125°=55°.
∵PB、PC分别是∠ABC和∠ACB的角平分线,
∴∠ABC+∠ACB=2(∠PBC+∠PCB)=2×55°=110°,
在△ABC中,∠A=180°-(∠ABC+∠ACB)=180°-110°=70°.
故答案为70°.
点评 本题主要利用三角形的内角和定理和角平分线的定义求解,熟练掌握定理和角平分线的定义是解题的关键.

练习册系列答案
 亮点激活精编提优100分大试卷系列答案
亮点激活精编提优100分大试卷系列答案
相关题目
11.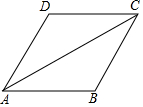 如图,菱形ABCD的周长是24,∠BAD=60°,则对角线AC的长等于( )
如图,菱形ABCD的周长是24,∠BAD=60°,则对角线AC的长等于( )
 如图,菱形ABCD的周长是24,∠BAD=60°,则对角线AC的长等于( )
如图,菱形ABCD的周长是24,∠BAD=60°,则对角线AC的长等于( )| A. | 3 | B. | 6 | C. | 3$\sqrt{3}$ | D. | 6$\sqrt{3}$ |
18. 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
①AD∥BC;
②∠ACB=2∠ADB;
③∠ADC=90°-∠ABD;
④∠BDC=$\frac{1}{2}$∠BAC.
其中正确的结论有( )
 如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:
如图,∠ABC=∠ACB,AD、BD、CD分别平分△ABC的外角∠EAC、内角∠ABC、外角∠ACF.以下结论:①AD∥BC;
②∠ACB=2∠ADB;
③∠ADC=90°-∠ABD;
④∠BDC=$\frac{1}{2}$∠BAC.
其中正确的结论有( )
| A. | 2个 | B. | 3个 | C. | 4个 | D. | 1 个 |
8.以下代数式书写规范的是( )
| A. | (x+y)÷2 | B. | 1$\frac{1}{3}$x | C. | $\frac{6}{5}$y | D. | m+n厘米 |
13.已知∠α与∠β互补,∠α=5∠β,则∠α等于( )
| A. | 150° | B. | 120° | C. | 90° | D. | 60° |
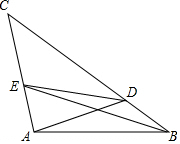 △ABC中,D在BC上,E在AC上,∠BAC=100°,∠ABC=40°,∠BAC=20°,∠ABE=20°,则∠ADE=30°.
△ABC中,D在BC上,E在AC上,∠BAC=100°,∠ABC=40°,∠BAC=20°,∠ABE=20°,则∠ADE=30°.