题目内容
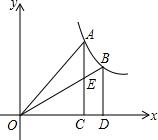如图，过反比例函数y=| 2 |
| x |
考点：反比例函数系数k的几何意义
专题：计算题
分析：根据反比例函数k的几何意义得到S△AOC=S△BOD，然后利用S四边形ABDO=S1+S△BDO=S2+S△AOC即可得到S1=S2．
解答：解：∵AC⊥x轴，BD⊥x轴，
∴S△AOC=S△BOD，
∵S四边形ABDO=S1+S△BDO=S2+S△AOC，
∴S1=S2．
故答案为S1=S2．
∴S△AOC=S△BOD，
∵S四边形ABDO=S1+S△BDO=S2+S△AOC，
∴S1=S2．
故答案为S1=S2．
点评：本题考查了反比例函数比例系数k的几何意义：在反比例函数y=xk图象中任取一点，过这一个点向x轴和y轴分别作垂线，与坐标轴围成的矩形的面积是定值|k|．
练习册系列答案
相关题目
判断下列语句错误的是（ ）
| A、棱柱、球是立体图形，角、直线、三角形、圆是平面图形 |
| B、两点的所有连线中，线段最短 |
| C、经过平面上任意两点有且只有两条直线 |
| D、把一条射线绕着它的端点旋转而形成的图形叫做角 |
9：30分时，钟表上的时针与分针所夹的锐角度数为（ ）
| A、60° | B、75° |
| C、90° | D、105° |
如图，∠AOD是直角，BO平分∠AOC，∠AOB：∠COD=2：5，求∠AOB的度数．
如图，已知EO⊥AB于点O，OE平分∠MON，那么∠1与∠2相等吗？为什么？
如图，数轴A、B上两点分别对应实数a、b，则下列结论正确的是（ ）| A、a+b＞0 | ||||
| B、ab＞0 | ||||
C、
| ||||
D、
|
如图所示，抛物线y=-x2+mx+n经过点A（1，0）和点C（4，0），与y轴交于点B．
在△ABC中，BO、CO分别平分∠CBA、∠BCA，求证：∠COB=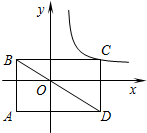
如图，矩形ABCD的对角线BD经过坐标原点，矩形的边分别平行于坐标轴，点C在反比例函数y=