题目内容
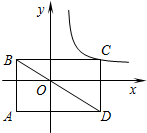 如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=
如图,矩形ABCD的对角线BD经过坐标原点,矩形的边分别平行于坐标轴,点C在反比例函数y=| k2+2k+1 |
| x |
| A、1 | B、-1或3 |
| C、4 | D、1或-3 |
考点:反比例函数图象上点的坐标特征
专题:
分析:根据矩形的对角线将矩形分成面积相等的两个直角三角形,找到图中的所有矩形及相等的三角形,即可推出S四边形CEOF=S四边形HAGO,根据反比例函数比例系数的几何意义即可求出k2+4k+1=4,再解出k的值即可.
解答: 解:如图:
解:如图:
∵四边形ABCD、HBEO、OECF、GOFD为矩形,
又∵BO为四边形HBEO的对角线,OD为四边形OGDF的对角线,
∴S△BEO=S△BHO,S△OFD=S△OGD,S△CBD=S△ADB,
∴S△CBD-S△BEO-S△OFD=S△ADB-S△BHO-S△OGD,
∴S四边形HAGO=S四边形CEOF=2×2=4,
∴xy=k2+2k+1=4,
解得k=1或k=-3.
故选D.
 解:如图:
解:如图:∵四边形ABCD、HBEO、OECF、GOFD为矩形,
又∵BO为四边形HBEO的对角线,OD为四边形OGDF的对角线,
∴S△BEO=S△BHO,S△OFD=S△OGD,S△CBD=S△ADB,
∴S△CBD-S△BEO-S△OFD=S△ADB-S△BHO-S△OGD,
∴S四边形HAGO=S四边形CEOF=2×2=4,
∴xy=k2+2k+1=4,
解得k=1或k=-3.
故选D.
点评:本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
 永乾教育寒假作业快乐假期延边人民出版社系列答案
永乾教育寒假作业快乐假期延边人民出版社系列答案
相关题目
已知下列命题:①两条直线被第三条直线所截,如果同位角相等,那么两直线平行;②相等的角是对顶角;③同角的余角相等;④三角形的一个外角等于和它不相邻的两个内角和.其中真命题有( )
| A、1个 | B、2个 | C、3个 | D、4个 |
若关于x的一元二次方程的两个根为x1=1,x2=2,则这个方程是( )
| A、x2+3x-2=0 |
| B、x2-3x+2=0 |
| C、x2-3x+3=0 |
| D、x2+3x+2=0 |
下列方程可能是一元一次方程的是( )
| A、2x+y=9 | ||
| B、x2-3x=1 | ||
C、
| ||
D、
|
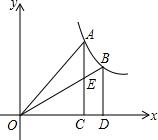 如图,过反比例函数y=
如图,过反比例函数y=