题目内容
 如图,在Rt△ABC中,∠C=90°,BC=8cm,AB=10cm,若P从点B出发以2cm/s的速度向A移动,动点Q从A出发以1cm/s的速度向C移动.设P、Q同时分别从B、A同时出发,其中一点到达终点则P、Q均停止运动,设运动时间为ts,解答下列问题.
如图,在Rt△ABC中,∠C=90°,BC=8cm,AB=10cm,若P从点B出发以2cm/s的速度向A移动,动点Q从A出发以1cm/s的速度向C移动.设P、Q同时分别从B、A同时出发,其中一点到达终点则P、Q均停止运动,设运动时间为ts,解答下列问题.(1)PQ∥BC时,求t的值;
(2)当t为何值时,△APQ与以AQ为腰的等腰三角形?
考点:平行线分线段成比例,等腰三角形的判定
专题:动点型
分析:(1)如图1,先利用勾股定理计算出AC=6,根据平行线分线段成比例,由PQ∥BC得
=
,即
=
,然后解方程即可;
(2)作QH⊥PA于H,如图2,根据等腰三角形的性质得AH=PH=
AP=5-t,再证明Rt△AQH∽Rt△ABC,根据相似的性质得到
=
,然后解方程即可.
| PA |
| AB |
| AQ |
| AC |
| 10-2t |
| 10 |
| t |
| 6 |
(2)作QH⊥PA于H,如图2,根据等腰三角形的性质得AH=PH=
| 1 |
| 2 |
| t |
| 10 |
| 5-t |
| 6 |
解答: 解:(1)如图1,∵∠C=90°,BC=8,AB=10,
解:(1)如图1,∵∠C=90°,BC=8,AB=10,
∴AC=
=6,
PB=2t,AQ=t,则AP=10-2t,
∵PQ∥BC,
∴
=
,即
=
,
∴t=
(s);
(2)①当AQ=PQ时, 作QH⊥PA于H,如图2,
作QH⊥PA于H,如图2,
∵△APQ是以AQ为腰的等腰三角形,
∴AH=PH=
AP=
(10-2t)=5-t,
∵∠QAH=∠BAC,
∴Rt△AQH∽Rt△ABC,
∴
=
,即
=
,
∴t=
(s).
②同理,当AQ=AP时,t=
s.
综上所述,当t=
或t=
s时,△APQ与以AQ为腰的等腰三角形.
 解:(1)如图1,∵∠C=90°,BC=8,AB=10,
解:(1)如图1,∵∠C=90°,BC=8,AB=10,∴AC=
| AB2-BC2 |
PB=2t,AQ=t,则AP=10-2t,
∵PQ∥BC,
∴
| PA |
| AB |
| AQ |
| AC |
| 10-2t |
| 10 |
| t |
| 6 |
∴t=
| 30 |
| 11 |
(2)①当AQ=PQ时,
 作QH⊥PA于H,如图2,
作QH⊥PA于H,如图2,∵△APQ是以AQ为腰的等腰三角形,
∴AH=PH=
| 1 |
| 2 |
| 1 |
| 2 |
∵∠QAH=∠BAC,
∴Rt△AQH∽Rt△ABC,
∴
| AQ |
| AB |
| AH |
| AC |
| t |
| 10 |
| 5-t |
| 6 |
∴t=
| 25 |
| 8 |
②同理,当AQ=AP时,t=
| 10 |
| 3 |
综上所述,当t=
| 25 |
| 8 |
| 10 |
| 3 |
点评:本题考查了平行线分线段成比例:三条平行线截两条直线,所得的对应线段成比例.也考查了等腰三角形的判定.

练习册系列答案
相关题目
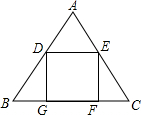 如图,等边三角形ABC中,G、F是BC边上两点,点D、E分别在边AB和AG上,四边形DGFE是长方形,若BG=1,AD=3,则BC=
如图,等边三角形ABC中,G、F是BC边上两点,点D、E分别在边AB和AG上,四边形DGFE是长方形,若BG=1,AD=3,则BC=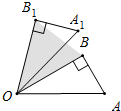 如图,在Rt△OAB中,∠B=90°,∠AOB=30°,将△OAB绕点O逆时针旋转α得到△OA1B1,当△OBB1的面积为1时,OB=2时,α的度数为
如图,在Rt△OAB中,∠B=90°,∠AOB=30°,将△OAB绕点O逆时针旋转α得到△OA1B1,当△OBB1的面积为1时,OB=2时,α的度数为