题目内容
已知(x+y)2=9,(x-y)2=1,求下列各式的值:
(1)x2+y2;
(2)xy;
(3)x4+y4.
(1)x2+y2;
(2)xy;
(3)x4+y4.
考点:完全平方公式
专题:
分析:(1)根据完全平方公式,可得和的平方、差的平方,根据和的平方加差的平方,可得2(x2+y2),根据等式的性质,可得答案;
(2)根据完全平方公式,可得和的平方、差的平方,根据和的平方减差的平方,可得2xy,根据等式的性质,可得答案;
(3)根据和的平方的平方减积的平方的2倍,可得答案.
(2)根据完全平方公式,可得和的平方、差的平方,根据和的平方减差的平方,可得2xy,根据等式的性质,可得答案;
(3)根据和的平方的平方减积的平方的2倍,可得答案.
解答:解:(x+y)2═x2+2xy+y2=9,(x-y)2=x2-2xy+y2=1
(1)x2+y2=[(x2+2xy+y2)+(x2-2xy+y2)]÷2=(9+1)÷2=5;
(2)xy═[(x2+2xy+y2)-(x2-2xy+y2)]÷4=(9-1)÷4=2;
(3)x4+y4=(x2+y2)2-2(xy)2=52-2×22=25-8=17.
(1)x2+y2=[(x2+2xy+y2)+(x2-2xy+y2)]÷2=(9+1)÷2=5;
(2)xy═[(x2+2xy+y2)-(x2-2xy+y2)]÷4=(9-1)÷4=2;
(3)x4+y4=(x2+y2)2-2(xy)2=52-2×22=25-8=17.
点评:本题考查了完全平方公式,利用了和的平方,差的平方公式.

练习册系列答案
相关题目
 已知四边形EFGH相似于四边形KLMN,各边长如图所示,求∠E,∠G,∠N的度数以及x,y,z的值.
已知四边形EFGH相似于四边形KLMN,各边长如图所示,求∠E,∠G,∠N的度数以及x,y,z的值.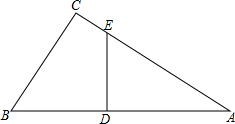 如图,在Rt△ABC中,∠C=90°,ED⊥AB.求证:∠AED=∠B.
如图,在Rt△ABC中,∠C=90°,ED⊥AB.求证:∠AED=∠B. 如图,在Rt△ABC中,∠C=90°,BC=8cm,AB=10cm,若P从点B出发以2cm/s的速度向A移动,动点Q从A出发以1cm/s的速度向C移动.设P、Q同时分别从B、A同时出发,其中一点到达终点则P、Q均停止运动,设运动时间为ts,解答下列问题.
如图,在Rt△ABC中,∠C=90°,BC=8cm,AB=10cm,若P从点B出发以2cm/s的速度向A移动,动点Q从A出发以1cm/s的速度向C移动.设P、Q同时分别从B、A同时出发,其中一点到达终点则P、Q均停止运动,设运动时间为ts,解答下列问题.