题目内容
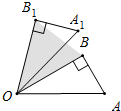 如图,在Rt△OAB中,∠B=90°,∠AOB=30°,将△OAB绕点O逆时针旋转α得到△OA1B1,当△OBB1的面积为1时,OB=2时,α的度数为
如图,在Rt△OAB中,∠B=90°,∠AOB=30°,将△OAB绕点O逆时针旋转α得到△OA1B1,当△OBB1的面积为1时,OB=2时,α的度数为考点:旋转的性质
专题:计算题
分析:作BC⊥OB1于C,如图,根据旋转的性质得∠BOB1=α,OB1=OB=2,在Rt△OBC中,利用正弦的定义得到BC=2sinα,然后根据三角形面积公式得
•OB1•BC=1,即
•2•2sinα=1,再利用特殊角的三角函数值求α.
| 1 |
| 2 |
| 1 |
| 2 |
解答:解: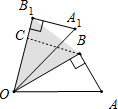 作BC⊥OB1于C,如图,
作BC⊥OB1于C,如图,
∵△OAB绕点O逆时针旋转α得到△OA1B1,
∴∠BOB1=α,OB1=OB=2,
在Rt△OBC中,∵sin∠BOC=sinα=
,
∴BC=2sinα,
∵△OBB1的面积为1,
∴
•OB1•BC=1,即
•2•2sinα=1,
∴sinα=
,
∴α=30°.
故答案为30°.
 作BC⊥OB1于C,如图,
作BC⊥OB1于C,如图,∵△OAB绕点O逆时针旋转α得到△OA1B1,
∴∠BOB1=α,OB1=OB=2,
在Rt△OBC中,∵sin∠BOC=sinα=
| BC |
| OB |
∴BC=2sinα,
∵△OBB1的面积为1,
∴
| 1 |
| 2 |
| 1 |
| 2 |
∴sinα=
| 1 |
| 2 |
∴α=30°.
故答案为30°.
点评:本题考查了旋转的性质:对应点到旋转中心的距离相等;对应点与旋转中心所连线段的夹角等于旋转角;旋转前、后的图形全等.也考查了三角形面积公式和锐角三角函数的定义.

练习册系列答案
相关题目
 如图,在Rt△ABC中,∠C=90°,BC=8cm,AB=10cm,若P从点B出发以2cm/s的速度向A移动,动点Q从A出发以1cm/s的速度向C移动.设P、Q同时分别从B、A同时出发,其中一点到达终点则P、Q均停止运动,设运动时间为ts,解答下列问题.
如图,在Rt△ABC中,∠C=90°,BC=8cm,AB=10cm,若P从点B出发以2cm/s的速度向A移动,动点Q从A出发以1cm/s的速度向C移动.设P、Q同时分别从B、A同时出发,其中一点到达终点则P、Q均停止运动,设运动时间为ts,解答下列问题.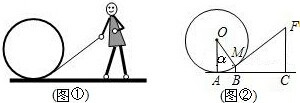 如图,图①是一个小朋友玩“滚铁环”的游戏.铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为25厘米,设铁环中心为O,铁环钩FM与铁环相切于点M,铁环与地面接触点为A,∠MOA=α,且sinα=0.6.
如图,图①是一个小朋友玩“滚铁环”的游戏.铁环是圆形的,铁环向前滚动时,铁环钩保持与铁环相切.将这个游戏抽象为数学问题,如图②.已知铁环的半径为25厘米,设铁环中心为O,铁环钩FM与铁环相切于点M,铁环与地面接触点为A,∠MOA=α,且sinα=0.6. 在四边形ABCD中,已知BC=8,CD=12,AD=10,∠A=∠B=60°,则AB=
在四边形ABCD中,已知BC=8,CD=12,AD=10,∠A=∠B=60°,则AB=