题目内容
1.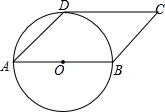 如图,四边形ABCD是平行四边形,∠C=45°,以AB为直径的⊙O经过点D,求证:CD是⊙O的切线.
如图,四边形ABCD是平行四边形,∠C=45°,以AB为直径的⊙O经过点D,求证:CD是⊙O的切线.
分析 连结OD,如图,根据平行四边形的性质得∠A=∠C=45°,AB∥CD,加上∠ODA=∠A=45°,则可判断OD⊥AB,再根据平行线的性质得OD⊥CD,然后根据切线的判定定理即可得到结论.
解答 证明:连结OD,如图,
∵四边形ABCD是平行四边形,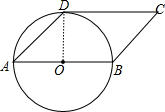
∴∠A=∠C=45°,AB∥CD,
∵OA=OD,
∴∠ODA=∠A=45°,
∴∠AOD=90°,
∴OD⊥AB,
∵CD∥AB,
∴OD⊥CD,
∴CD是⊙O的切线.
点评 本题考查了切线的判定定理:经过半径的外端且垂直于这条半径的直线是圆的切线.要证某线是圆的切线,已知此线过圆上某点,连接圆心与这点(即为半径),再证垂直即可.也考查了平行四边形的性质.

练习册系列答案
 名师导航单元期末冲刺100分系列答案
名师导航单元期末冲刺100分系列答案 名校名卷单元同步训练测试题系列答案
名校名卷单元同步训练测试题系列答案
相关题目
5.已知二次函数y=ax2+bx+c中,函数y与自变量x的部分对应值如下表:
(1)求该二次函数的表达式;
(2)若A(-4,y1),B($\frac{11}{2}$,y2)两点都在该函数的图象上,试比较y1与y2的大小.
| x | … | -1 | 0 | 1 | 2 | 4 | … |
| y | … | 0 | -3 | -4 | -3 | 5 | … |
(2)若A(-4,y1),B($\frac{11}{2}$,y2)两点都在该函数的图象上,试比较y1与y2的大小.
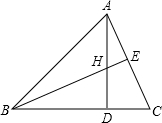 如图,H是△ABC的高AD、BE的交点,且DH=DC.给出下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD.其中正确的是( )
如图,H是△ABC的高AD、BE的交点,且DH=DC.给出下列结论:①BD=AD;②BC=AC;③BH=AC;④CE=CD.其中正确的是( ) 已知:如图,AB=CB,AD=CD,求证:∠A=∠C.
已知:如图,AB=CB,AD=CD,求证:∠A=∠C. 如图,BE,CD是△ABC的高,且BE=CD,求证:△BCD≌△CBE.
如图,BE,CD是△ABC的高,且BE=CD,求证:△BCD≌△CBE.