题目内容
12. 已知抛物线y=ax2-2x+c的对称轴为直线x=-1,顶点为A,与y轴正半轴交点为B,且△ABO的面积为1.
已知抛物线y=ax2-2x+c的对称轴为直线x=-1,顶点为A,与y轴正半轴交点为B,且△ABO的面积为1.(1)求抛物线的表达式;
(2)若点P在x轴上,且PA=PB,求点P的坐标.
分析 (1)根据对称轴求得a,然后根据三角形面积求得c,即可求得解析式;
(2)设P点的坐标为(x,0),根据PA=PB得出关于x的方程,解方程求得x的值,进而求得点P的坐标.
解答 解:(1)∵对称轴为直线x=-1,
∴-$\frac{-2}{2a}$=-1,
∴a=-1,
∵△ABO的面积为1,
∴$\frac{1}{2}$c×1=1,
∴c=2,
∴抛物线的表达式为y=-x2-2x+2;
(2)∵y=-x2-2x+2=-(x+1)2+3,
∴A(-1,3),
设P点的坐标为(x,0).
∵PA=PB,B(0,2),
∴(x+1)2+32=x2+22,
解得x=-3.
故P点的坐标为(-3,0).
点评 本题考查了待定系数法求二次函数的解析式,两点间的距离公式,x轴上点的坐标特征,根据PA=PB列出方程是解题的关键.

练习册系列答案
 文敬图书课时先锋系列答案
文敬图书课时先锋系列答案
相关题目
20. 如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
 如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )
如图,在△ABC中,∠ACB=90°,分别以点A和B为圆心,以相同的长(大于$\frac{1}{2}$AB)为半径作弧,两弧相交于点M和N,作直线MN交AB于点D,交BC于点E,连接CD,下列结论错误的是( )| A. | AD=BD | B. | BD=CD | C. | ∠A=∠BED | D. | ∠ECD=∠EDC |

 如图,在△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D是BC边上一点,直线ED⊥BC于点D,交AB于点E,CF∥AB交直线DE于点F,设CD=x
如图,在△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D是BC边上一点,直线ED⊥BC于点D,交AB于点E,CF∥AB交直线DE于点F,设CD=x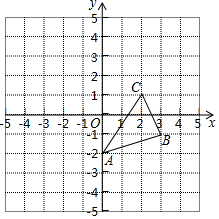 如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,-2),B(3,-1),C(2,1).
如图,图中的小方格都是边长为1的正方形,△ABC的顶点坐标为A(0,-2),B(3,-1),C(2,1).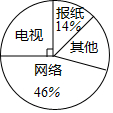 小明为了解他所居住小区居民最近“接受信息的最主要渠道”,利用课余时间,问卷调查了他所居住小区的居民,数据整理后,绘制成如下的扇形统计图.如果填写“接受信息的最主要渠道”是“网络”的人数有276名,试问:
小明为了解他所居住小区居民最近“接受信息的最主要渠道”,利用课余时间,问卷调查了他所居住小区的居民,数据整理后,绘制成如下的扇形统计图.如果填写“接受信息的最主要渠道”是“网络”的人数有276名,试问: