题目内容
2.如果点P1(x1,y1),P2(x2,y2),P3(x3,y3)在某双曲线上,且x1<x2<0<x3,则y1,y2,y3的大小关系可能为( )| A. | y1<y2<y3 | B. | y1>y2>y3 | C. | y2<y3<y1 | D. | y3>y2>y1 |
分析 先根据反比例函数的解析式判断出函数图象所在的象限,再根据在每一象限内的增减性进行解答即可.
解答 解:设反比例函数的解析式为y=$\frac{k}{x}$,
①当k>0时,双曲线在一,三象限,在每个象限内,y随x的增大而减小,
∵x1<x2<0<x3,∴y1>y2>0,y3<0,
∴y1>y2>y3,
②当k<0时,双曲线在二,四象限,在每个象限内,y随x的增大而增大,
∵x1<x2<0<x3,
∴0<y1<y2,y3<0,
∴y3<0<y1<y2,
故选B.
点评 本题考查的是反比例函数图象上点的坐标特点,熟知反比例函数图象上各点的坐标一定适合此函数的解析式是解答此题的关键.

练习册系列答案
相关题目
12.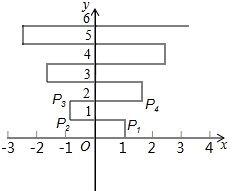 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第99次跳动至点P99的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第99次跳动至点P99的坐标是( )
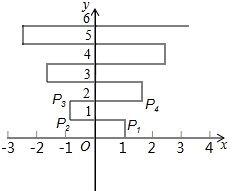 如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第99次跳动至点P99的坐标是( )
如图,在平面直角坐标系上有个点P(1,0),点P第1次向上跳动1个单位至点P1(1,1),紧接着第2次向左跳动2个单位至点P2(-1,1),第3次向上跳动1个单位,第4次向右跳动3个单位,第5次又向上跳动1个单位,第6次向左跳动4个单位,…,依此规律跳动下去,点P第99次跳动至点P99的坐标是( )| A. | (26,50) | B. | (-26,50) | C. | (25,50) | D. | (-25,50) |
13.下列说法;①线段的垂直平分线是它的对称轴;②角的对称轴是角的平分线;③平面上的两条相交直线是轴对称图形,它只有一条对称轴;④直线是轴对称图形,它有无数条对称轴.其中正确的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
11.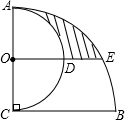 如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )
 如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )
如图,AC⊥BC,AC=BC=4,以AC为直径作半圆,圆心为点O;以点C为圆心,BC为半径作弧AB,过点O作BC的平行线交两弧于点D、E,则阴影部分的面积是( )| A. | $\frac{5}{3}π-2\sqrt{3}$ | B. | $\frac{5}{3}π-4$ | C. | $3π-2\sqrt{3}$ | D. | 3π-4 |
3.整数8与12的最大公因数是( )
| A. | 1 | B. | 2 | C. | 4 | D. | 24 |
 如图,在△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D是BC边上一点,直线ED⊥BC于点D,交AB于点E,CF∥AB交直线DE于点F,设CD=x
如图,在△ABC中,∠ACB=90°,AC=2,BC=2$\sqrt{3}$,D是BC边上一点,直线ED⊥BC于点D,交AB于点E,CF∥AB交直线DE于点F,设CD=x


