题目内容
3.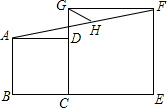 如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=3,H是AF的点,则GH的长是( )
如图,正方形ABCD和正方形CEFG中,点D在CG上,BC=2,CE=3,H是AF的点,则GH的长是( )| A. | 1 | B. | $\sqrt{2}$ | C. | $\frac{\sqrt{2}}{2}$ | D. | 1.5 |
分析 连接DH并延长交GF于M,由ASA证明△ADH≌△FMH,得出对应边DH=MH,AD=FM=2,证出△DGM是等腰直角三角形,由三角函数求出DM,再由直角三角形斜边上的中线性质即可得出结果.
解答 解:连接DH并延长交GF于M,如图所示: ∵四边形ABCD和四边形CEFG是正方形,
∵四边形ABCD和四边形CEFG是正方形,
∴AD=BC=CD=2,GF=CG=CE=3,∠ADC=∠ADG=∠DGD=90°,
∴DG=1,AD∥GF,
∴∠DAH=∠MFH,
∵H是AF的中点,
∴AH=FH,
在△ADH和△FMH中,$\left\{\begin{array}{l}{∠DAH=∠MFH}&{\;}\\{AH=FH}&{\;}\\{∠AHD=∠FHM}&{\;}\end{array}\right.$,
∴△ADH≌△FMH(ASA),
∴DH=MH,AD=FM=2,
∴GM=GF-FM=1,
∴DG=GM,
∴△DGM是等腰直角三角形,
∴DM=$\sqrt{2}$DG=$\sqrt{2}$,
∵∠DGM=90°,DH=MH,
∴GH=$\frac{1}{2}$DM=$\frac{\sqrt{2}}{2}$;
故选:C.
点评 本题考查了全等三角形的判定与性质、正方形的性质、等腰直角三角形的判定与性质、直角三角形斜边上的中线性质;熟练掌握正方形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
 阶梯计算系列答案
阶梯计算系列答案
相关题目
7.在平面直角坐标系中,把点P(-5,3)向右平移8个单位得到点P1,再将点P1绕原点旋转90°得到点P2,则点P2的坐标是( )
| A. | (3,-3) | B. | (-3,3) | C. | (3,3)或(-3,-3) | D. | (3,-3)或(-3,3) |
8.下列说法错误的是( )
| A. | -2的相反数是2 | B. | 3的倒数是$\frac{1}{3}$ | ||
| C. | (-3)-(-5)=2 | D. | -11,0,4这三个数中最小的数是0 |
8.南京长江隧道即将通车,这将大大改善市民过江难的问题.已知隧道洞长37900米,这个数用科学记数法可表示为( )
| A. | 3.79×103 | B. | 3.79×104 | C. | 3.79×105 | D. | 0.379×106 |
13.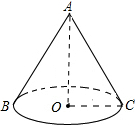 如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )
如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )
 如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )
如图,已知圆锥的底面周长为6πcm,高为4cm,则这个圆锥的全面积是( )| A. | 9π | B. | 24π | C. | 15π | D. | 30π |
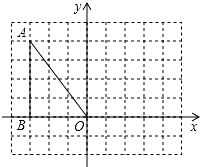 如图,已知点A(-3,4),B(-3,0),将△OAB绕原点O顺时针旋转90°,得到△OA1B1.
如图,已知点A(-3,4),B(-3,0),将△OAB绕原点O顺时针旋转90°,得到△OA1B1.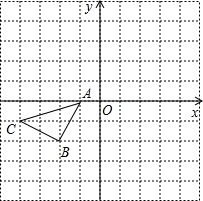 如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题:
如图所示的正方形网格中,△ABC的顶点均在格点上,在所给直角坐标系中解答下列问题: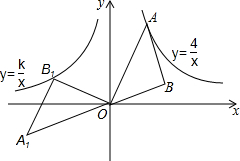 如图,A是反比例函数y=$\frac{4}{x}$(x>0)图象上一点,以OA为斜边作等腰直角△ABO,将△ABO绕点O以逆时针旋转135°,得到△A1B1O,若反比例函数y=$\frac{k}{x}$的图象经过点B1,则k的值是-2.
如图,A是反比例函数y=$\frac{4}{x}$(x>0)图象上一点,以OA为斜边作等腰直角△ABO,将△ABO绕点O以逆时针旋转135°,得到△A1B1O,若反比例函数y=$\frac{k}{x}$的图象经过点B1,则k的值是-2.