若x+y=$\sqrt{3\sqrt{5}-\sqrt{2}}$.x-y=$\sqrt{3\sqrt{2}-\sqrt{5}}$.求xy．题目和参考答案——青夏教育精英家教网—

题目内容

18．若x+y=$\sqrt{3\sqrt{5}-\sqrt{2}}$，x-y=$\sqrt{3\sqrt{2}-\sqrt{5}}$，求xy．

分析将等式两边分别平方，然后再相减，从而可求得xy的值．

解答解：∵x+y=$\sqrt{3\sqrt{5}-\sqrt{2}}$，x-y=$\sqrt{3\sqrt{2}-\sqrt{5}}$，
∴（x+y）²=3$\sqrt{5}$-$\sqrt{2}$①，（x-y）²=3$\sqrt{2}$-$\sqrt{5}$②．
∴①-②得；4xy=$4\sqrt{5}$-4$\sqrt{2}$．
∴xy=$\sqrt{5}-\sqrt{2}$．

点评本题主要考查的是二次根式的化简求值、完全平方公式的应用，平方法的应用是解题的关键．

练习册系列答案

9．抛物线①y=3x²，②y=$\frac{2}{3}$x²，③y=-$\frac{4}{3}$x²的开口大小的次序应为：①③②．

6．

如图，△ADC≌△AFB，∠DAB=20°，DA∥BF，DC、BF交于E，∠FEC=110°．
（1）求∠FAC的度数；
（2）AF平行于DC吗？说明理由；
（3）求∠BAC的度数．

13．

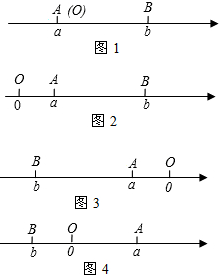阅读材料：点A、B在数轴上分别表示实数a、b，A、B两点之间的距离表示为|AB|，当两点中有一点在原点时，不妨设点A在原点．如图1．|AB|=|OB|=|b|=|a-b|；当A，B两点都不在原点时，
①如图（2），点A，B都在原点的右边，|AB|=|OB|-|OA|=|b|-|a|=b-a=|a-b|；
②如图（3），点A，B都在原点的左边，|AB|=|OB|-|OA|=|b|-|a|=-b-（-a）=|a-b|；
③如图（4），点A，B在原点的两边，|AB|=|OA|+|OB|=|a|+|b|=a+（-b）=|a-b|；
综上，数轴上A，B两点之间的距离|AB|=|a-b|．
请你仿照上例，回答下列问题：
①数轴上表示-2和-5的两点之间的距离是3；数轴上表示1和-3的两点之间的距离是4；
②数轴上表示x和-1的两点A和B之间的距离是|x+1|，如果|AB|=2，那么x为1或-3；
③当-3＜x＜2时，|x+3|+|x+2|=1或2x+5；
④当代数式|x-2|+|x+1|取最小值时，相应的x的取值范围是-1≤x≤2；
⑤|x-1|+|x-2|+|x-3|+…+|x-2010|最小值是1010025．

3．

如图，在△ABC中，BC=12，∠BAC=100°，AB的垂直平分线交BC于点E，交AB于点D，AC的垂直平分线交BC于点N，交AC于点M．
（1）求△AEN的周长．
（2）求∠EAN的度数．
（3）如果DE交MN于点P，猜想△PBC的形状．

10．若m、n互为相反数，a，b互为负倒数，则（m+n）•$\frac{a}{b}$-ab=1．

16．铁路上，长300米的货车以每秒20米的速度匀速行驶，迎面有一长2O0米的客车以每秒30米的速度驶过来，间两车相遇时的错车时间是多少？

17．

已知，如图，△ABC中，AB=AC，D是三角形外一点，DE⊥AB于E，DF⊥AC于F，且DE=DF，求证：EF∥BC．

试题分类