题目内容
3. 如图,在△ABC中,BC=12,∠BAC=100°,AB的垂直平分线交BC于点E,交AB于点D,AC的垂直平分线交BC于点N,交AC于点M.
如图,在△ABC中,BC=12,∠BAC=100°,AB的垂直平分线交BC于点E,交AB于点D,AC的垂直平分线交BC于点N,交AC于点M.(1)求△AEN的周长.
(2)求∠EAN的度数.
(3)如果DE交MN于点P,猜想△PBC的形状.
分析 (1)由线段垂直平分线的性质可知:BE=AE,AN=NC,从而求得△AEN的周长;
(2)由三角形的内角和定理求得∠B+∠C=80°,然后根据等腰三角形的性质可知∠BAE+∠NAC=80°,故此可求得∠EAN=20°;
(3)连接AP、BP、CP,由线段垂直平分线的性质可知;PB=PA=PC,从而得到PB=PC.
解答 解:(1)∵DE是AB的垂直平分线,
∴AE=BE.
同理;AN=NC.
∴△AEN的周长=AE+EN+AN=BE+EN+NC=BC=12.
(2)∵AE=BE,AN=NC,
∴∠B=∠BAE,∠C=∠CAN.
∵∠BAC=100°,
∴∠B+∠C=80°.
∴∠BAE+∠NAC=80°.
∴∠EAN=100°-80°=20°;
(3)如图所示:连接PA、PB、PC.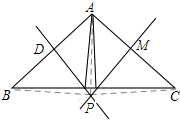
∵DP垂直平分AB,
∴PA=PB.
同理:PA=PC.
∴PB=PC.
∴△PBC为等腰三角形.
点评 本题主要考查的是线段垂直平分线的性质、等腰三角形的性质和判定、三角形的内角和定理,掌握线段垂直平分线的性质是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
1.给出下列表格:
根据表中信息,y关于x的函数解析式可以是y=3x-2.
| x | … | -2 | -1 | 0 | 1 | 2 | … |
| y | … | -8 | -5 | -2 | 1 | 4 | … |
 已知,如图,△ABC和△ADE是底边在同一条直线上的两个等腰三角形,求证:CD=BE.
已知,如图,△ABC和△ADE是底边在同一条直线上的两个等腰三角形,求证:CD=BE. 如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合)PM,PN分别垂直于CD,AB,垂足分别为M,N,若⊙O的半径长度为2,则MN的长为$\sqrt{3}$.
如图,直径AB,CD的夹角为60°,P为⊙O上的一个动点(不与点A,B,C,D重合)PM,PN分别垂直于CD,AB,垂足分别为M,N,若⊙O的半径长度为2,则MN的长为$\sqrt{3}$.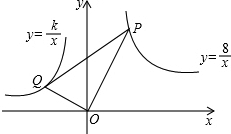 如果y=$\frac{8}{x}$过P点,y=$\frac{k}{x}$过Q点,OP⊥OQ,OP=2OQ,Q(m,1),则S△OPQ=5.
如果y=$\frac{8}{x}$过P点,y=$\frac{k}{x}$过Q点,OP⊥OQ,OP=2OQ,Q(m,1),则S△OPQ=5.