题目内容
10．已知等腰三角形的一条腰长是5，底边上的高为4，则它的面积为12．分析 利用等腰三角形的性质结合勾股定理得出BC的长，进而求出它的面积．
解答 
解：如图所示：过点A作AD⊥BC于点D，
由题意可得：AB=AC=5，AD=4，
则在Rt△ABD中，BD=DC=$\sqrt{A{B}^{2}-A{D}^{2}}$=3，
故S△ABC=$\frac{1}{2}$×6×4=12．
故答案为：12．
点评 此题主要考查了勾股定理以及等腰三角形的性质，得出BC的长是解题关键．
练习册系列答案
举一反三期末百分冲刺卷系列答案
相关题目
1．化简$\frac{{m}^{2}-3m}{{m}^{2}-9}$的结果是（ ）
| A． | $\frac{m}{m-3}$ | B． | $\frac{m}{m+3}$ | C． | $\frac{m}{3-m}$ | D． | -$\frac{m}{m•3}$ |
5．一项工程由甲工程队单独完成需要12天，由乙工程队单独完成需要16天，甲工程队单独施工5天后，为加快工程进度，又抽调乙工程队加入该工程施工，问还需多少天可以完成该工程？如果设还需x天可以完成该工程，则可列方程为（ ）
| A． | $\frac{5+x}{12}+\frac{x}{16}=1$ | B． | $\frac{x}{12}+\frac{5+x}{16}=1$ | C． | 12（5+x）+16x=1 | D． | 12（5+x）=16x |
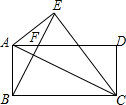如图，在矩形ABCD中，BC=2BA=8，将矩形ABCD沿AC所在直线翻折使△ABC与△AEC重合，连接BE，BE交AD于点F，则线段EF的长为$\frac{6\sqrt{5}}{5}$．
20．下列说法中，正确的是（ ）
| A． | 有理数就是正数和负数的统称 | B． | 一个有理数不是整数就是分数 | ||
| C． | 零是最小的整数 | D． | 正分数、零、负分数统称分数 |