题目内容
19.记M(1)=-2,M(2)=(-2)×(-2),M(3)=(-2)×(-2)×(-2),…M(n)=$\underset{\underbrace{(-2)×(-2)×…×(-2)}}{n个-2相乘}$(1)计算:M(5)+M(6);
(2)求2M(2015)+M(2016)的值:
(3)说明2M(n)与M(n+1)互为相反数.
分析 (1)根据M(n)=$\underset{\underbrace{(-2)×(-2)×…×(-2)}}{n个-2相乘}$,可得M(5),M(6),;根据有理数的加法,可得答案;
(2)根据乘方的意义,可得M(2015),M(2016),根据有理数的加法,可得答案;
(3)根据乘方的意义,可得M(n),M(n+1),根据有理数的加法,可得答案.
解答 解:(1)M(5)+M(6)=(-2)5+(-2)6=-32+64=32;
(2)2M(2015)+M(2016)=2×(-2)2015+(-2)2016=-(-2)×(-2)2015+(-2)2016=-(-2)2016+(-2)2016=0;
(3)2M(n)+M(n+1)=-(-2)×(-2)n+(-2)n+1=-(-2)n+1+(-2)n+1=0,
∴2M(n)与M(n+1)互为相反数.
点评 本题考查了同底数幂的乘法,利用了同底数幂的乘法,相反数的性质:互为相反数的和为零.

练习册系列答案
相关题目
4.在下列方程组中,不是二元一次方程组的是( )
| A. | $\left\{\begin{array}{l}{x-3y=3}\\{y=-1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{x+1=3}\\{y+2=-1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{x+2y=3}\\{3x-2y=-1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{\frac{x}{y}=3}\\{x-y=4}\end{array}\right.$ |
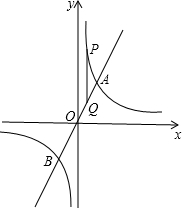 如图,已知直线y=kx(k>0)与双曲线y=$\frac{8}{x}$交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点P(1,a),过点P作PQ∥y轴交直线AB于点Q.
如图,已知直线y=kx(k>0)与双曲线y=$\frac{8}{x}$交于A、B两点,且点A的纵坐标为4,第一象限的双曲线上有一点P(1,a),过点P作PQ∥y轴交直线AB于点Q.