题目内容
19.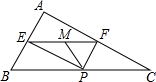 如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )
如图,在△ABC中,∠BAC=90°,AB=3,AC=4,P为边BC上一动点,PE⊥AB于E,PF⊥AC于F,M为EF的中点,则PM的最小值为( )| A. | 1.2 | B. | 1.3 | C. | 1.4 | D. | 2.4 |
分析 先求证四边形AFPE是矩形,再根据直线外一点到直线上任一点的距离,垂线段最短,利用相似三角形对应边成比例即可求得AP最短时的长,然后即可求出PM最短时的长.
解答 解:连结AP,如图所示:
∵∠BAC=90°,AB=3,AC=4,
∴BC=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∵PE⊥AB,PF⊥AC,
∴四边形AFPE是矩形,
∴EF=AP.
∵M是EF的中点,
∴PM=$\frac{1}{2}$AP,
根据直线外一点到直线上任一点的距离,垂线段最短,
即AP⊥BC时,AP最短,同样PM也最短,
∴当AP⊥BC时,AP=$\frac{3×4}{5}$=2.4,
∴AP最短时,AP=2.4,
∴当PM最短时,PM=$\frac{1}{2}$AP=1.2.
故选A.
点评 此题主要考查了勾股定理、矩形的判定与性质、垂线段最短和直角三角形斜边上的中线性质;由直角三角形的面积求出AP是解决问题的关键.

练习册系列答案
相关题目
9.要使代数式$\frac{{\sqrt{1-x}}}{x+2}$有意义,则x的取值范围是( )
| A. | x≥1 | B. | x≤1 | C. | x≥1且x≠-2 | D. | x≤1且x≠-2 |
10.一直角三角形的斜边长为15cm,其中一直角边长为5cm,则这个三角形的面积为( )
| A. | 25$\sqrt{2}$cm2 | B. | 50$\sqrt{2}$cm2 | C. | $\frac{75}{2}c{m}^{2}$ | D. | 75cm2 |
11.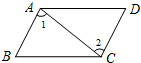 如图,∠1=∠2,∠DAB=∠BCD.下列四个结论中,错误的是( )
如图,∠1=∠2,∠DAB=∠BCD.下列四个结论中,错误的是( )
 如图,∠1=∠2,∠DAB=∠BCD.下列四个结论中,错误的是( )
如图,∠1=∠2,∠DAB=∠BCD.下列四个结论中,错误的是( )| A. | AB∥CD | B. | AD∥BC | C. | ∠B=∠D | D. | ∠DCA=∠DAC |
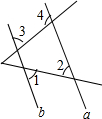 如图,∠1=60°,∠2=60°,∠3=80°,求∠4的度数.
如图,∠1=60°,∠2=60°,∠3=80°,求∠4的度数.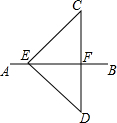 如图,已知AB是线段CD的垂直平分线,E是AB上一点,如果EC=10,EF=8,那么DF=6.
如图,已知AB是线段CD的垂直平分线,E是AB上一点,如果EC=10,EF=8,那么DF=6.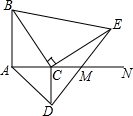 如图所示,线段AB=8cm,射线AN⊥AB于点A,点C是射线上一动点,分别以AC、BC为直角边作等腰直角三角形,得△ACD与△BCE中,连接DE交射线AN于点M,则CM的长为4.
如图所示,线段AB=8cm,射线AN⊥AB于点A,点C是射线上一动点,分别以AC、BC为直角边作等腰直角三角形,得△ACD与△BCE中,连接DE交射线AN于点M,则CM的长为4.