题目内容
14.解方程组:$\left\{\begin{array}{l}{\frac{4}{3x-2y}+\frac{3}{2x-5y}=10}\\{\frac{5}{3x-2y}-\frac{2}{2x-5y}=1}\end{array}\right.$.分析 设$\frac{1}{3x-2y}$=a,$\frac{1}{2x-5y}$=b,方程组变形为关于a与b的方程组,求出解得到a与b的值,即可求出x与y的值.
解答 解:设$\frac{1}{3x-2y}$=a,$\frac{1}{2x-5y}$=b,
方程组变形得:$\left\{\begin{array}{l}{4a+3b=10①}\\{5a-2b=1②}\end{array}\right.$,
①×2+②×3得:23a=23,即a=1,
把a=1代入①得:b=2,
可得$\left\{\begin{array}{l}{3x-2y=1}\\{2x-5y=\frac{1}{2}}\end{array}\right.$,即$\left\{\begin{array}{l}{3x-2y=1①}\\{4x-10y=1②}\end{array}\right.$,
①×5-②得:11x=4,即x=$\frac{4}{11}$,
把x=$\frac{4}{11}$代入①得:y=$\frac{1}{22}$,
经检验,方程组的解为$\left\{\begin{array}{l}{x=\frac{4}{11}}\\{y=\frac{1}{22}}\end{array}\right.$.
点评 此题考查了解二元一次方程组,利用了换元的思想,熟练掌握运算法则是解本题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.若$\frac{1}{4}$-ax+x2是一个完全平方式,则常数a的值为( )
| A. | -$\frac{1}{2}$ | B. | $±\frac{1}{2}$ | C. | 1 | D. | ±1 |
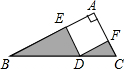 如图,Rt△ABC中,∠A=90°,四边形AEDF为正方形,E、D、F分别在Rt△ABC的三边上,BD=3,CD=2,则图中阴影部分的面积之和为3.
如图,Rt△ABC中,∠A=90°,四边形AEDF为正方形,E、D、F分别在Rt△ABC的三边上,BD=3,CD=2,则图中阴影部分的面积之和为3. 如图用相同的小长方形壁砖铺满周长为500cm的大长方形电视机背景墙,求小长方形的长和宽.
如图用相同的小长方形壁砖铺满周长为500cm的大长方形电视机背景墙,求小长方形的长和宽.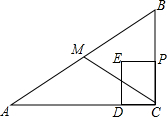 如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点M是边AB的中点,连结CM,点P从点C出发,以1cm/s的速度沿CB运动到点B停止,以PC为边作正方形PCDE,点D落在线段AC上.设点P的运动时间为t(s).
如图,在Rt△ABC中,∠ACB=90°,AC=8cm,BC=6cm,点M是边AB的中点,连结CM,点P从点C出发,以1cm/s的速度沿CB运动到点B停止,以PC为边作正方形PCDE,点D落在线段AC上.设点P的运动时间为t(s).