题目内容
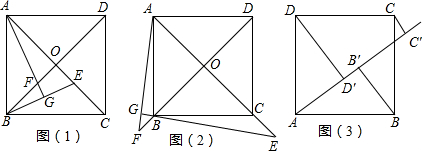
3.如图(1)所示,已知正方形ABCD的对角线AC,BD相交于O,E是AC上一点,过A作AG⊥BE,垂足为G,AG交BD于F;(1)试证明:OE=OF
(2)对于上述命题,若点E在AC的延长线上,AG⊥BE交BE的延长线于点G,AG的延长线交DB的延长线于点F,其他条件不变,如图(2)所示,则结论“OE=OF”还成立吗?如果成立,请给出证明,如果不成立,请说明理由;
(3)如图(3),正方形ABCD的边长为1,点P为边BC上任意一点(可与点B或点C重合),分别过点B、C、D作射线AP的垂线,垂足分别为点B′、C′、D′.求:BB′+CC′+DD′的最大值和最小值.
分析 (1)由同角的余角相等,可得∠EBD=∠GAE,由正方形的性质知,AO=BO,∠AOB=∠BOE,则ASA证得△AFO≌△BEO,可得OE=OF;
(2)思路与(1)相同,易得△AFO≌△BEO,可得OE=OF;
(3)找到S四边形BCDA=S△ABP+S△ADP+S△DPC的等量关系,并且根据本等量关系计算得BB′+CC′+DD′=$\frac{2}{AP}$,根据AP的范围计算BB′+CC′+DD′的最小值和最大值.
解答 (1)证明:在正方形ABCD中AO=BO,∠AOB=∠BOE,
又∵AG⊥BE,
∴∠GAE+∠BEA=90°,∠EBD+∠AEB=90°.
∴∠EBD=∠GAE.
在△AOF和△BOE中,
$\left\{\begin{array}{l}{∠AOF=∠BOE}\\{AO=BO}\\{∠OAF=∠OBE}\end{array}\right.$
∴△AOF≌△BOE(ASA).
∴OE=OF.
(2)OE=OF仍成立.
证明:在正方形ABCD中AO=BO,∠AOB=∠BOE,
又∵AG⊥BE,
∴∠GAE+∠BEA=90°,∠EBD+∠AEB=90°.
∴∠EBD=∠GAE.
在△AOF和△BOE中,
$\left\{\begin{array}{l}{∠AOF=∠BOE}\\{AO=BO}\\{∠OAF=∠OBE}\end{array}\right.$,
∴△AOF≌△BOE(ASA).
∴OE=OF.
(3)解:如图,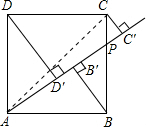
∵S△DPC=S△APC=$\frac{1}{2}$AP•CC′,
得S四边形BCDA=S△ABP+S△ADP+S△DPC
=$\frac{1}{2}$AP(BB′+DD′+CC′),
于是BB′+CC′+DD′=$\frac{2}{AP}$.
又∵1≤AP≤$\sqrt{2}$,
∴$\sqrt{2}$≤BB′+CC′+DD′≤2,
∴BB′+CC′+DD′的最小值为$\sqrt{2}$,最大值为2.
点评 此题考查四边形的综合题,要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,正确利用勾股定理,三角形的面积解决问题.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 天水历史悠久,文物古迹星罗棋布,是中国历史文化名城,也是中国优秀旅游城市.如图是秦州区的部分旅游景点,请你以中心广场为坐标原点建立坐标系,并写出各景点的坐标:
天水历史悠久,文物古迹星罗棋布,是中国历史文化名城,也是中国优秀旅游城市.如图是秦州区的部分旅游景点,请你以中心广场为坐标原点建立坐标系,并写出各景点的坐标: 如图,∠COD在∠AOB的内部绕点O进行旋转,∠AOD+∠BOC=110°,∠AOC+∠BOD=50°,OE,OF分别是∠AOC与∠BOD的平分线.
如图,∠COD在∠AOB的内部绕点O进行旋转,∠AOD+∠BOC=110°,∠AOC+∠BOD=50°,OE,OF分别是∠AOC与∠BOD的平分线.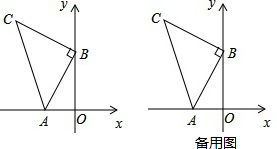
 如图是边长为1的正方形网格,点A、B、C、D都在格点上,图中阴影部分的面积等于15.
如图是边长为1的正方形网格,点A、B、C、D都在格点上,图中阴影部分的面积等于15.