题目内容
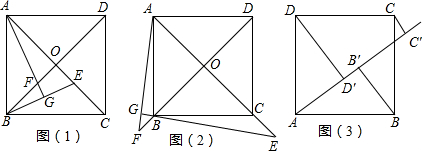
13. 如图是边长为1的正方形网格,点A、B、C、D都在格点上,图中阴影部分的面积等于15.
如图是边长为1的正方形网格,点A、B、C、D都在格点上,图中阴影部分的面积等于15.
分析 如图,观察图形容易发现:直接求出阴影部分的面积比较困难,故将其转化为:求矩形MNPQ的面积减去四个小三角形的面积之差,即可解决问题.
解答  解:如图,
解:如图,
SABCD=SMNPQ-S△ABM-S△BCQ-S△CDP-S△ADN
=6×5-$\frac{1}{2}×3×4-\frac{1}{2}×2×3-\frac{1}{2}×5×2-\frac{1}{2}×2×1$
=30-15=15.
故答案为15.
点评 该题主要考查了三角形的面积公式及其应用问题;解题的方法是牢固掌握三角形的面积公式,这是灵活运用的基础和关键.

练习册系列答案
相关题目
1.在平面直角坐标系中,点P的坐标为(4,5),则点P在( )
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
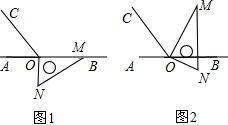
3. 如图,CO⊥AB,垂足为点O,若∠1=∠2,则∠DOE等于( )
如图,CO⊥AB,垂足为点O,若∠1=∠2,则∠DOE等于( )
 如图,CO⊥AB,垂足为点O,若∠1=∠2,则∠DOE等于( )
如图,CO⊥AB,垂足为点O,若∠1=∠2,则∠DOE等于( )| A. | 60° | B. | 80° | C. | 90° | D. | 100° |
 如图,A、B之间是一座山,一条高速公路要通过A、B两点,在A地测得公路走向是北偏东70°32′.如果A、B两地同时开工,则:
如图,A、B之间是一座山,一条高速公路要通过A、B两点,在A地测得公路走向是北偏东70°32′.如果A、B两地同时开工,则: