题目内容
5.已知xy>0,将$\sqrt{-\frac{y}{{x}^{2}}}$化为最简二次根式为( )| A. | $\frac{\sqrt{y}}{x}$ | B. | $\frac{\sqrt{-y}}{x}$ | C. | $\frac{-\sqrt{y}}{x}$ | D. | $\frac{-\sqrt{-y}}{x}$ |
分析 首先判断出x的符号,然后依据二次根式的性质进行化简即可.
解答 解:∵二次根式被开方数大于等于0可知:-$\frac{y}{{x}^{2}}$≥0,
有∵xy>0,
∴y<0,x<0.
∴原式=$\frac{\sqrt{-y}}{\sqrt{{x}^{2}}}$=$\frac{\sqrt{-y}}{-x}$.
故选:D.
点评 本题主要考查的是二次根式的性质的应用,掌握二次根式的性质是解题的关键.

练习册系列答案
相关题目
13.纳米(nm)是非常小的长度单位,已知1nm=10-6mm,某种病毒的直径是100nm,若将这种病毒排成1mm长,则病毒的个数是( )
| A. | 102个 | B. | 104个 | C. | 106个 | D. | 108个 |
20.下列各式中,运算结果等于x2-4x-12的是( )
| A. | (x+3)(x-4) | B. | (x-2)(x+6) | C. | (x-3)(x+4) | D. | (x+2)(x-6) |
14.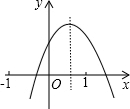 抛物线y=ax2+bx+c图象如图,有下列7个结论:
抛物线y=ax2+bx+c图象如图,有下列7个结论:
①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+c>0;⑥a+b>m(am+b)(m≠1);⑦9a-3b+c<0
其中错误的有( )
 抛物线y=ax2+bx+c图象如图,有下列7个结论:
抛物线y=ax2+bx+c图象如图,有下列7个结论:①abc>0;②b<a+c;③4a+2b+c>0;④2c<3b;⑤a+c>0;⑥a+b>m(am+b)(m≠1);⑦9a-3b+c<0
其中错误的有( )
| A. | 3个 | B. | 4个 | C. | 5个 | D. | 6个 |
15.若|a+3|+(b-2)2=0,则ab的值为( )
| A. | -9 | B. | 9 | C. | -8 | D. | 8 |
 如图,在△ABC中,D是BC边上的点,AD=DC,∠BAD=40°,∠C=35°,求证:△ABD是等腰三角形.
如图,在△ABC中,D是BC边上的点,AD=DC,∠BAD=40°,∠C=35°,求证:△ABD是等腰三角形.