题目内容
2.如图甲,平面直角坐标系中,边长为2的正方形ABCD顶点A与原点重合,边AB、AD落在坐标轴上,在正方形内有AE=2,过点E作直线MN⊥AE交BC、CD分别于M、N,连接AM、AN.(1)在图甲中,直接写出:∠MAN=45°,△MCN的周长=4.
(2)在图甲中,设BM=x,求DN的长(用含x的式子表示).
(3)若线段AE=2在正方形外(只考虑第三象限),请在图乙中作出相应的图形,探索线段BM、MN、DN三者之间的关系并给出证明.

分析 (1)证得Rt△AEN≌Rt△ADN,Rt△ABM≌△AEN,得出∠EAN=∠DAN,∠BAM=∠EAM,EN=DN,ME=BM,得出∠MAN=45°,△MCN的周长=4;
(2)由Rt△AEN≌Rt△ADN,Rt△ABM≌△AEN,得到EN=DN,ME=BM,设BM=x,DN=m,则MC=2-x,CN=2-m,在Rt△CMN中,利用勾股定理CM2+CN2=MN2,即可解答;
(3)连接AM,证Rt△AEM≌Rt△ABM,连接AN,证Rt△AEN≌Rt△ADN,从而得DN=BM+MN;
解答 解:(1)∠MAN=45°,△MCN的周长=4;
故答案为:45,4;
(2)∵Rt△AEN≌Rt△ADN,Rt△ABM≌△AEN,
∴EN=DN,ME=BM,
设BM=x,DN=m,则MC=2-x,CN=2-m,
∴MN=x+m,
在Rt△CMN中,CM2+CN2=MN2
即(2-x)2+(2-m)2=(x+m)2
解得:m=$\frac{4-2x}{x+2}$
即DN=$\frac{4-2x}{x+2}$.
(3)如图乙,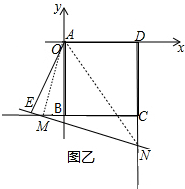
连接AM,AN,
在Rt△AEM和Rt△ABM中,
$\left\{\begin{array}{l}{AE=AD}\\{AM=AM}\end{array}\right.$,
∴Rt△AEM≌Rt△ABM,
∴EM=BM,
在Rt△AEN和Rt△ADN中,
$\left\{\begin{array}{l}{AE=AD}\\{AN=AN}\end{array}\right.$,
∴Rt△AEN≌Rt△ADN,
∴DN=NE=MN+ME=MN+BM,
即DN=BM+MN.
点评 此题考查四边形的综合题,综合考查了正方形的性质,三角形全等的判定与性质,勾股定理以及三角形的面积计算,正确做出辅助线,掌握三角形全等的判定方法是解决问题的关键.

| A. | A′(3,3),B′(0,0) | B. | A′(-2,-2),B′(0,0) | C. | A′(3,3),B′(5,5) | D. | A′(3,3),B′(-5,5) |
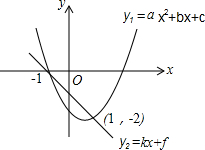 若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )
若二次函数y1=ax2+bx+c与一次函数y2=kx+f的图象如图所示,当y1<y2时,关于x的取值范围,有可能是下列不等式组解中的(其中mn<0)( )| A. | $\left\{\begin{array}{l}{mx<1}\\{nx>1}\end{array}\right.$ | B. | $\left\{\begin{array}{l}{mx>1}\\{nx>1}\end{array}\right.$ | C. | $\left\{\begin{array}{l}{mx>1}\\{nx<1}\end{array}\right.$ | D. | $\left\{\begin{array}{l}{mx<1}\\{nx<1}\end{array}\right.$ |
| A. | -a3 | B. | a3 | C. | a7 | D. | a10 |
| A. | 0个 | B. | 1个 | C. | 2个 | D. | 3个 |
| A. | a≥0 | B. | a≤0 | C. | a≥1 | D. | a≤1 |
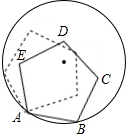 如图,边长为1的正五边形ABCDE,顶点A、B在半径为1的圆上,其它各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为12°.
如图,边长为1的正五边形ABCDE,顶点A、B在半径为1的圆上,其它各点在圆内,将正五边形ABCDE绕点A逆时针旋转,当点E第一次落在圆上时,则点C转过的度数为12°.