题目内容
 已知:如图,B,C,B三点在同一条直线上,AC∥DE,AB=CD,∠ACD=∠B.若AC=3,DE=5,求BE的长.
已知:如图,B,C,B三点在同一条直线上,AC∥DE,AB=CD,∠ACD=∠B.若AC=3,DE=5,求BE的长.考点:全等三角形的判定与性质
专题:计算题
分析:由AC与DE平行,利用两直线平行同位角相等得到一对角相等,再由∠ACD=∠B,利用外角性质及等量代换得到一对角相等,以及AB=CD,利用AAS得到三角形ABC与三角形CDE全等,利用全等三角形的对应边相等得到BC=DE=5,EC=AC=3,由BE=BC+CE即可求出BE的长.
解答:解:∵AC∥DE,
∴∠ACB=∠E,
∵∠ACD=∠B,∠ACE=∠ACD+∠DCE=∠A+∠B,
∴∠DCE=∠A,
在△ABC和△CDE中,
,
∴△ABC≌△CDE(AAS),
∴BC=DE=5,EC=AC=3,
则BE=BC+CE=3+5=8.
∴∠ACB=∠E,
∵∠ACD=∠B,∠ACE=∠ACD+∠DCE=∠A+∠B,
∴∠DCE=∠A,
在△ABC和△CDE中,
|
∴△ABC≌△CDE(AAS),
∴BC=DE=5,EC=AC=3,
则BE=BC+CE=3+5=8.
点评:此题考查了全等三角形的判定与性质,熟练掌握全等三角形的判定与性质是解本题的关键.

练习册系列答案
 口算能手系列答案
口算能手系列答案
相关题目
 如图所示的几何体的主视图是( )
如图所示的几何体的主视图是( )A、 |
B、 |
C、 |
D、 |
 如图,在△ABC中,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H.
如图,在△ABC中,BC=5,高AD=4,矩形EFPQ的一边QP在BC边上,E、F分别在AB、AC上,AD交EF于点H.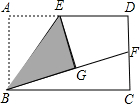 如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,再延长BG交DC于点F.
如图,在矩形ABCD中,E是AD的中点,将△ABE沿BE折叠后得到△GBE,且点G在矩形ABCD内部,再延长BG交DC于点F. 如图,直线AB∥CD,∠GEB的平分线EF交CD于点F,∠HGF=40°,求∠EFD的度数.
如图,直线AB∥CD,∠GEB的平分线EF交CD于点F,∠HGF=40°,求∠EFD的度数. 仔细阅读完成下列问题:
仔细阅读完成下列问题: