题目内容
20.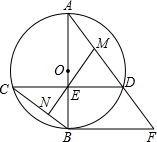 如图,AB为⊙O直径,且弦CD⊥AB于点E,过点B作⊙O的切线与AD的延长线交于点F.
如图,AB为⊙O直径,且弦CD⊥AB于点E,过点B作⊙O的切线与AD的延长线交于点F.(1)若EN⊥BC于点N,延长NE与AD相交于点M.求证:AM=MD;
(2)若⊙O的半径为10,且cosC=$\frac{4}{5}$,求切线BF的长.
分析 (1)想办法证明AM=EM,DM=EM即可解决问题;
(2)求出AF=$\frac{5}{4}AB=\frac{5}{4}×20=25$,根据BF=$\sqrt{A{F}^{2}-A{B}^{2}}$计算即可解决问题;
解答 (1)证法一:∵∠A与∠C对同弧BD,
∴∠A=∠C,
∵CD⊥AB于点E,
∴∠CEB=90°.
∴∠C+∠CBE=90°.
∵MN⊥BC,
∴∠ENB=90°.
∴∠NEB+∠CBE=90°.
∴∠C=∠NEB,
∵∠NEB=∠AEM,
∴∠AEM=∠A,
∴AM=ME,
∵∠AEM=∠A,
∠MED+∠AEM=90°,
∠EDA+∠A=90°,
∴∠MED=∠EDA,
∴ME=MD,
∴AM=MD.
证法二:∵∠CDA与∠CBA对同弧AC,
∴∠CDA=∠CBA,
∵CD⊥AB于点E,
∴∠AED=90°,
∴∠MED+∠MEA=90°,
∵MN⊥BC,
∴∠ENB=90°,
∴∠CBA+∠BEN=90°,
∵∠MEA=∠BEN,
∴∠MED=∠CBA,
∴∠MED=∠CDA,
∴ME=MD,
∵∠MED+∠AEM=90°,
∠CDA+∠A=90°,
∴∠AEM=∠A,
∴AM=ME,
∴AM=MD.
(2)解:∵BF与⊙O相切于点B,
∴AB⊥BF.
∴∠ABF=90°.
∵∠C与∠A对同弧BD,
∴∠C=∠A,
∴cosA=cosC=$\frac{4}{5}$,
∴cosA=$\frac{AB}{AF}$=$\frac{4}{5}$,
∴AF=$\frac{5}{4}AB=\frac{5}{4}×20=25$,
∴BF=$\sqrt{A{F}^{2}-A{B}^{2}}$=$\sqrt{2{5}^{2}-2{0}^{2}}$=15.
点评 本题考查切线的性质、垂径定理、勾股定理、锐角三角函数、解直角三角形等知识,解题的关键是灵活运用所学知识解决问题,所以中考常考题型.

| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
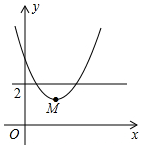 如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )
如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )| A. | 0个或1个 | B. | 0个或2个 | C. | 1个或2个 | D. | 0个、1个或2个 |
 如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( )
如图,矩形ABCD中,AB=10,BC=8,P为AD的中点,将△ABP沿BP翻折至△EBP(点A落到点E处),连接DE,则图中与∠APB相等的角的个数为( )