题目内容
13.已知α、β是关于x的一元二次方程x2-(2m+3)x+m2=0的两个不相等的实数根,且满足$\frac{1}{α}$+$\frac{1}{β}$=1,则m的值是( )| A. | 3 | B. | -1 | C. | 3或-1 | D. | -3或1 |
分析 由根与系数的关系结合$\frac{1}{α}$+$\frac{1}{β}$=1,可得出关于m的分式方程,解之即可得出m的值,再根据根的判别式△>0,即可得出m的值,此题得解.
解答 解:∵α、β是关于x的一元二次方程x2-(2m+3)x+m2=0的两个的实数根,
∴α+β=2m+3,αβ=m2,
∴$\frac{1}{α}$+$\frac{1}{β}$=$\frac{α+β}{αβ}$=$\frac{2m+3}{{m}^{2}}$=1,
解得:m=-1或m=3,
经检验,m=-1或m=3均为原分式方程的解.
∵α、β是关于x的一元二次方程x2-(2m+3)x+m2=0的两个不相等的实数根,
∴△=[-(2m+3)]2-4m2=12m+9>0,
∴m>-$\frac{3}{4}$,
∴m=3.
故选A.
点评 本题考查根与系数的关系以及根的判别式,根据根与系数的关系结合$\frac{1}{α}$+$\frac{1}{β}$=1,找出关于m的分式方程是解题的关键.

练习册系列答案
相关题目
8.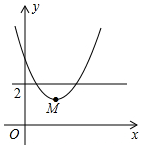 如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )
如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )
 如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )
如图,平面直角坐标系中,点M是直线y=2与x轴之间的一个动点,且点M是抛物线y=$\frac{1}{2}{x^2}$+bx+c的顶点,则抛物线y=$\frac{1}{2}{x^2}$+bx+c与直线y=1交点的个数是( )| A. | 0个或1个 | B. | 0个或2个 | C. | 1个或2个 | D. | 0个、1个或2个 |
18.下列调查中,适宜采用普查方式的是( )
| A. | 对一批LED节能灯使用寿命的调查 | |
| B. | 对冷饮市场上冰淇淋质量情况的调查 | |
| C. | 对一个社区每天丢弃塑料袋数量的调查 | |
| D. | 对大型民用直升机各零部件的检查 |
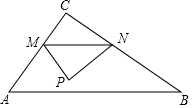 如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是相交.
如图,在Rt△ABC中,∠C=90°,AC≠BC,点M是边AC上的动点.过点M作MN∥AB交BC于N,现将△MNC沿MN折叠,得到△MNP.若点P在AB上.则以MN为直径的圆与直线AB的位置关系是相交. 将一个正方体如图放置在一个长方体上,则所构成的几何体的左视图可能是( )
将一个正方体如图放置在一个长方体上,则所构成的几何体的左视图可能是( )



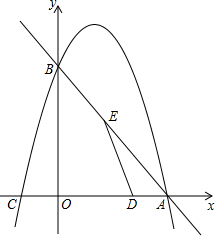 如图,在平面直角坐标系中,直线$y=-\frac{4}{3}x+8$与x轴,y轴分别交于点A、B,抛物线y=ax2-4ax+c经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0<t<5.
如图,在平面直角坐标系中,直线$y=-\frac{4}{3}x+8$与x轴,y轴分别交于点A、B,抛物线y=ax2-4ax+c经过点A和点B,与x轴的另一个交点为C,动点D从点A出发,以每秒1个单位长度的速度向O点运动,同时动点E从点B出发,以每秒2个单位长度的速度向A点运动,设运动的时间为t秒,0<t<5.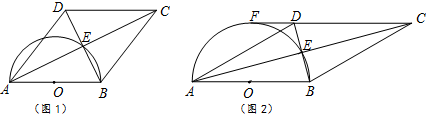
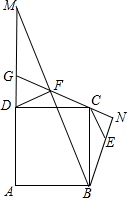 如图,等腰Rt△BNF的直角边FN所在的直线过正方形ABCD的顶点C,且与AD的延长线交于G,BF、AD的延长线交于M,连接DF,CE∥BM交BN于E.
如图,等腰Rt△BNF的直角边FN所在的直线过正方形ABCD的顶点C,且与AD的延长线交于G,BF、AD的延长线交于M,连接DF,CE∥BM交BN于E.