题目内容
(1)-
ab3c•
a3b3•(-8a2b3)
(2)(2x4y3-
x3y2+3x2y3)÷
x2y2
(3)x2-(x+2)(x-2)-(2x+1)2
(4)3(3m+2)2-2(2m+1)(2m-1)
| 5 |
| 3 |
| 3 |
| 10 |
(2)(2x4y3-
| 1 |
| 2 |
| 1 |
| 2 |
(3)x2-(x+2)(x-2)-(2x+1)2
(4)3(3m+2)2-2(2m+1)(2m-1)
考点:整式的混合运算
专题:
分析:(1)根据单项式的乘法法则进行计算即可;
(2)根据多项式除以单项式的法则进行计算即可;
(3)根据平方差公式和完全平方公式进行计算即可;
(4)根据平方差公式和完全平方公式进行计算即可.
(2)根据多项式除以单项式的法则进行计算即可;
(3)根据平方差公式和完全平方公式进行计算即可;
(4)根据平方差公式和完全平方公式进行计算即可.
解答:解:(1)原式=
×
×8a6b9c4
=4a6b9c4;
(2)原式=2x4y3÷
x2y2-
x3y2÷
x2y2+3x2y3÷
x2y2
=4x2y-x+6y;
(3)原式=x2-x2+4-4x2-4x-1
=-4x2-4x+3;
(4)原式=27m2+36m+12-8m2+2
=19m2+36m+14.
| 5 |
| 3 |
| 3 |
| 10 |
=4a6b9c4;
(2)原式=2x4y3÷
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
=4x2y-x+6y;
(3)原式=x2-x2+4-4x2-4x-1
=-4x2-4x+3;
(4)原式=27m2+36m+12-8m2+2
=19m2+36m+14.
点评:本题考查了整式的混合运算,熟练掌握平方差公式和完全平方公式是解题的关键.

练习册系列答案
 全能测控一本好卷系列答案
全能测控一本好卷系列答案 发散思维新课堂系列答案
发散思维新课堂系列答案
相关题目
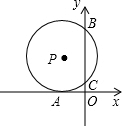 如图,⊙P的圆心在第二象限内,且与x轴相切于点A,与y轴相交于B(0,8)、C(0,2),则圆心P的坐标是( )
如图,⊙P的圆心在第二象限内,且与x轴相切于点A,与y轴相交于B(0,8)、C(0,2),则圆心P的坐标是( )| A、(-3,4) |
| B、(-4,6) |
| C、(-3,5) |
| D、(-4,5) |
计算(
)2003×1.52002×(-1)2004的结果是( )
| 2 |
| 3 |
A、
| ||
B、
| ||
C、-
| ||
D、-
|
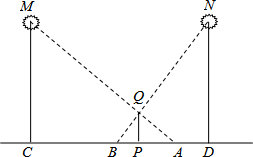 如图所示,某天晚上,身高1.8m的小明站在路灯M和路灯N之间的点P处,发现左右各有两个浅色的影子,其中靠近路灯M的影长BP=0.9m,靠近路灯N的影长PA=1.8m,已知路灯M和路灯N的高度一样,而且两者相距9m,问:路灯M的高度是多少?
如图所示,某天晚上,身高1.8m的小明站在路灯M和路灯N之间的点P处,发现左右各有两个浅色的影子,其中靠近路灯M的影长BP=0.9m,靠近路灯N的影长PA=1.8m,已知路灯M和路灯N的高度一样,而且两者相距9m,问:路灯M的高度是多少?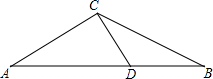 如图,在△ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,则∠A的度数是
如图,在△ABC中,AC=BC,在边AB上截取AD=AC,连接CD,若点D恰好是线段AB的一个黄金分割点,则∠A的度数是 如图,在正方形ABCD所在的平面内求一点P,使△PAB,△PBC,△PCD,△PAD都是等腰三角形,具有这性质的点P有
如图,在正方形ABCD所在的平面内求一点P,使△PAB,△PBC,△PCD,△PAD都是等腰三角形,具有这性质的点P有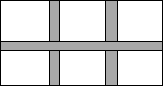 新园小区计划在一块长为40米,宽为26米的矩形场地上修建三条同样宽的甬路(两条纵向、一条横向,且横向、纵向互相垂直),其余部分种花草.若要使种花草的面积达到800m2,则甬路宽为多少米?设甬路宽为x米,则根据题意,可列方程为
新园小区计划在一块长为40米,宽为26米的矩形场地上修建三条同样宽的甬路(两条纵向、一条横向,且横向、纵向互相垂直),其余部分种花草.若要使种花草的面积达到800m2,则甬路宽为多少米?设甬路宽为x米,则根据题意,可列方程为