题目内容
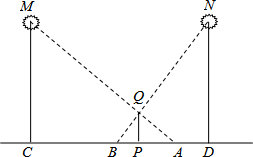 如图所示,某天晚上,身高1.8m的小明站在路灯M和路灯N之间的点P处,发现左右各有两个浅色的影子,其中靠近路灯M的影长BP=0.9m,靠近路灯N的影长PA=1.8m,已知路灯M和路灯N的高度一样,而且两者相距9m,问:路灯M的高度是多少?
如图所示,某天晚上,身高1.8m的小明站在路灯M和路灯N之间的点P处,发现左右各有两个浅色的影子,其中靠近路灯M的影长BP=0.9m,靠近路灯N的影长PA=1.8m,已知路灯M和路灯N的高度一样,而且两者相距9m,问:路灯M的高度是多少?考点:相似三角形的应用
专题:应用题
分析:设路灯M的高度为xm,则CM=DN=xm,根据平行线分线段成比例,由PQ∥CM得
=
,则AC=x,PC=x-1.8,再由PQ∥DN得
=
,则BD=
x,PD=BD-BP=
x-0.9,由于PC+PD=9,所以x-1.8+
x-0.9=9,然后解方程求出x即可.
| 1.8 |
| x |
| 1.8 |
| AC |
| 1.8 |
| x |
| 0.9 |
| BD |
| 1 |
| 2 |
| 1 |
| 2 |
| 1 |
| 2 |
解答:解:设路灯M的高度为xm,则CM=DN=xm,PQ=1.8m,
∵PQ∥CM,
∴
=
,即
=
,
∴AC=x,
∴PC=AC-AP=x-1.8,
∵PQ∥DN,
∴
=
,即
=
,
∴BD=
x,
∴PD=BD-BP=
x-0.9,
∵PC+PD=9,
∴x-1.8+
x-0.9=9,
解得x=7.8.
答:路灯M的高度是7.8m.
∵PQ∥CM,
∴
| PQ |
| CM |
| PA |
| AC |
| 1.8 |
| x |
| 1.8 |
| AC |
∴AC=x,
∴PC=AC-AP=x-1.8,
∵PQ∥DN,
∴
| PQ |
| DN |
| BP |
| BD |
| 1.8 |
| x |
| 0.9 |
| BD |
∴BD=
| 1 |
| 2 |
∴PD=BD-BP=
| 1 |
| 2 |
∵PC+PD=9,
∴x-1.8+
| 1 |
| 2 |
解得x=7.8.
答:路灯M的高度是7.8m.
点评:本题考查了相似三角形的应用:利用影长测量物体的高度;利用相似测量河的宽度(测量距离);借助标杆或直尺测量物体的高度.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
已知二次根式
与
是同类二次根式,则a的值可以是( )
| 2a-4 |
| 2 |
| A、6 | B、7 | C、8 | D、9 |
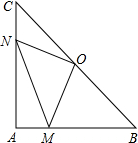 在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点. 如图,点A、B、C分别在线段OD、OE、OF上,且AB∥DE,BC∥EF
如图,点A、B、C分别在线段OD、OE、OF上,且AB∥DE,BC∥EF