题目内容
在矩形ABCD中,点E在直线AB上,连接DE,交对角线AC于点F,若AB=3,BC=4,BE=1,则FC的长为 .
考点:矩形的性质
专题:
分析:如图1、2,在图1中,首先求出AC的长度,然后证明△DFC∽△EFA,列出比例式即可解决问题;在图2中,类比上述解法,同理可求出线段CF的长.
解答: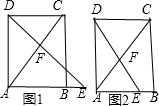 解:如图1,当点E在线段AB的延长线上时,
解:如图1,当点E在线段AB的延长线上时,
∵四边形ABCD是矩形,
∴∠ABC=90°,且AB=3,BC=4,
∴AC2=32+42=25,
∴AC=5;设CF=x,
则AF=5-x;
∵DC∥AE,
∴△DFC∽△EFA,
∴
=
,
即
=
,
解得:x=
.
如图2,当点E在AB边上时,
AE=3-1=2,类比图1,
同理可得:
=
,
即
=
,
解得:x=3,
综上所述,FC的长为
或3.
故答案为
或3.
 解:如图1,当点E在线段AB的延长线上时,
解:如图1,当点E在线段AB的延长线上时,∵四边形ABCD是矩形,
∴∠ABC=90°,且AB=3,BC=4,
∴AC2=32+42=25,
∴AC=5;设CF=x,
则AF=5-x;
∵DC∥AE,
∴△DFC∽△EFA,
∴
| DC |
| AE |
| CF |
| AF |
即
| 3 |
| 3+1 |
| x |
| 5-x |
解得:x=
| 15 |
| 7 |
如图2,当点E在AB边上时,
AE=3-1=2,类比图1,
同理可得:
| DC |
| AE |
| CF |
| AF |
即
| 3 |
| 2 |
| x |
| 5-x |
解得:x=3,
综上所述,FC的长为
| 15 |
| 7 |
故答案为
| 15 |
| 7 |
点评:该命题以矩形为载体,以考查矩形的性质、相似三角形的判定及其应用为线索构造而成;根据题意,运用分类讨论的数学思想,分两种情况来分析、判断、推理或解答.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
在二次根式
,
,
,
,
中,最简二次根式的个数是( )
| 72 |
| 5a3 |
| 3 |
| 9 |
|
| A、1个 | B、2个 | C、3个 | D、4个 |
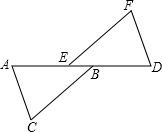 如图,点A、E、B、D在同一条直线上,在△ABC和△DEF中,BC=EF,AC∥DF,CB∥FE.连接AF、DC.线段AF、DC的关系是
如图,点A、E、B、D在同一条直线上,在△ABC和△DEF中,BC=EF,AC∥DF,CB∥FE.连接AF、DC.线段AF、DC的关系是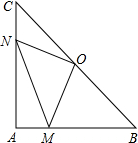 在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点.
在Rt△ABC中,AB=AC,∠BAC=90°,O为BC的中点. 如图,在△ABC中,AB=AC,AD是△ABC的角平分线,作AE∥BC,CE∥AD,AE、CE交于点E.
如图,在△ABC中,AB=AC,AD是△ABC的角平分线,作AE∥BC,CE∥AD,AE、CE交于点E.