题目内容
14. 将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表
将一个正三角形纸片剪成四个全等的小正三角形,再将其中的一个按同样的方法剪成四个更小的正三角形,…如此继续下去如图,结果如表| 所剪次数 | 1 | 2 | 3 | 4 | … | n |
| 正三角形个数 | 4 | 7 | 10 | 13 | … | an |
| A. | 2n | B. | 3(n-1) | C. | 3(n+1) | D. | 3n+1 |
分析 根据图跟表我们可以看出n代表所剪次数,an代表小正三角形的个数,也可以根据图形找出规律加以求解.
解答 解:由图可知没剪的时候,有一个三角形,以后每剪一次就多出三个,
所以总的个数3n+1.
故选:D.
点评 本题主要考查图形的变化规律,根据表格得出每剪一次就多出三个三角形是解题的关键.

练习册系列答案
 新课标阶梯阅读训练系列答案
新课标阶梯阅读训练系列答案
相关题目
2.下列事件中属于必然事件的是( )
| A. | 任意买一张电影票,座位号是偶数 | B. | 367人中至少有2人的生日相同 | ||
| C. | 掷一次骰子,向上的一面是6点 | D. | 某射击运动员射击1次,命中靶心 |
6.己知二次函数y=ax2+bx+c(a>0),对任意实数t,其图象都经过点(2+t,m)和点(2-t,m),又图象经过点(-1,y1),(2,y2),(6,y3),则函数值y1,y2,y3的大小关系是( )
| A. | y1>y2>y3 | B. | y3>y1>y2 | C. | y2>y1>y3 | D. | y3>y2>y1 |
3.将5041精确到百位的结果是( )
| A. | 5000 | B. | 5.0×103 | C. | 50 | D. | 5.04×103 |
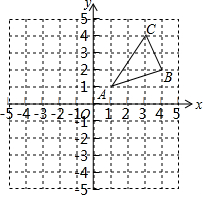 如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4).
如图,△ABC三个顶点的坐标分别为A(1,1),B(4,2),C(3,4). 如图,在正方形ABCD的对角线BD上取点E,使得∠BAE=75°,连接AE,CE,将线段CE绕点C顺时针旋转,使点E的对应点恰好落在AE延长线上的点F处.若AB=2,则AF的长为$\frac{4\sqrt{6}}{3}$.
如图,在正方形ABCD的对角线BD上取点E,使得∠BAE=75°,连接AE,CE,将线段CE绕点C顺时针旋转,使点E的对应点恰好落在AE延长线上的点F处.若AB=2,则AF的长为$\frac{4\sqrt{6}}{3}$.