题目内容
4．五一劳动节期间，小华和小刚骑车去离家28km远的公园游玩，从早晨6时30分出发，要在8时30分前到达，如果他每小时行驶xkm，可以得到的不等式为2x≥28，解得x的取值范围是x≥14．分析 要求实际每小时行驶多少千米，应求出路程和实际所用的时间．根据题意，路程为28千米，时间为最多2小时，进而得出答案．
解答 解：设他每小时要走x km，则可列不等式为：
2x≥28，
解得：x≥14，
故答案为：2x≥28，x≥14．
点评 此题主要考查了由实际问题抽象出一元一次不等式，利用关系式：速度×时间=路程是解题关键．
练习册系列答案
相关题目
14．
将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，…如此继续下去如图，结果如表
则an=（ ）（用含n的代数式表示）
将一个正三角形纸片剪成四个全等的小正三角形，再将其中的一个按同样的方法剪成四个更小的正三角形，…如此继续下去如图，结果如表| 所剪次数 | 1 | 2 | 3 | 4 | … | n |
| 正三角形个数 | 4 | 7 | 10 | 13 | … | an |
| A． | 2n | B． | 3（n-1） | C． | 3（n+1） | D． | 3n+1 |
15．已知（-1，y1），（1，y2）是直线y=-9x+6上的两个点，则y1，y2的大小关系是（ ）
| A． | y1＞0＞y2 | B． | y1＞y2＞0 | C． | y2＞0＞y1 | D． | 0＞y1＞y2 |
12．若a＜b，则下列各式中一定正确的是（ ）
| A． | a-b＞0 | B． | a+b＞0 | C． | ab＞0 | D． | -a＞-b |
如图，已知矩形ABCD中，FA、HB、FD、HC分别平分∠BAD、∠ABC、∠ADC、∠BCD．求证：四边形EFGH是正方形．
9．在Rt△ABC中，∠C=90°，AB=5，BC=3，则AC为（ ）
| A． | 4 | B． | 16 | C． | $\sqrt{34}$ | D． | 8 |
16．半径为1的圆的外切直角三角形的面积的最小值为（ ）
| A． | 3-$2\sqrt{2}$ | B． | 3+$2\sqrt{2}$ | C． | 6-4$\sqrt{2}$ | D． | 6+4$\sqrt{2}$ |
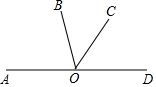如图，已知点O是直线AD上一点，且∠BOC=$\frac{1}{3}$∠AOC=$\frac{2}{3}$∠COD．求∠BOC的度数．
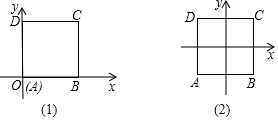已知正方形ABCD，边长为1cm．