题目内容
17．解下列不等式，并把解集在数轴上表示出来：（1）2（x-1）+5＜3x；
（2）$\frac{2-x}{4}$≥$\frac{1-x}{3}$．
分析 （1）先去括号，再移项、合并同类项，把x的系数化为1即可；
（2）先去分母，再去括号，再移项、再合并同类项1即可．
解答 解：（1）去括号得，2x-2+5＜3x，
移项得，2x-3x＜2-5，
合并同类项得，-x＜-3，
把x的系数化为1得，x＞3．
在数轴上表示为：
；
（2）去分母得，3（2-x）≥4（1-x）
去括号得，6-3x≥4-4x，
移项得，-3x+4x≥4-6，
合并同类项得，x≥-2．
在数轴上表示为：
．
点评 本题考查的是解一元一次不等式，熟知解一元一次不等式的基本步骤是解答此题的关键．
练习册系列答案
相关题目
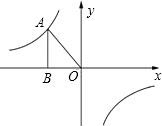如图所示，已知反比例函数y=$\frac{k}{x}$（k＜0）的图象经过点A（-$\sqrt{3}$，m），过点A作AB⊥x轴于点B，且△AOB的面积为2$\sqrt{3}$．
长方形ABCD中，∠ADB=20°，现将这一长方形纸片沿AF折叠，若使AB′∥BD，则折痕AF与AB的夹角∠BAF应为55°．
