题目内容
8.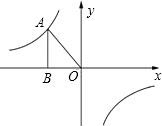 如图所示,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,m),过点A作AB⊥x轴于点B,且△AOB的面积为2$\sqrt{3}$.
如图所示,已知反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,m),过点A作AB⊥x轴于点B,且△AOB的面积为2$\sqrt{3}$.(1)求k和m的值;
(2)若一次函数y=ax+b的图象经过点A,并且与x轴相交于点C,且∠ACO=30°,求该直线的函数表达式.
分析 (1)把A(-$\sqrt{3}$,m)代入反比例函数,可得k=-$\sqrt{3}$m,且m>0,再根据△AOB的面积为2$\sqrt{3}$可得$\frac{1}{2}$×$\sqrt{3}$•m=2$\sqrt{3}$,解可得m,进而可求k;
(2)因为要满足∠ACO=30°这个条件,所以必须分类讨论:C点在负半轴、C点在正半轴.求C点坐标后再求直线解析式.
解答 解:(1)∵反比例函数y=$\frac{k}{x}$(k<0)的图象经过点A(-$\sqrt{3}$,m),
∴-$\sqrt{3}$m=k,且m>0,
∵AB⊥x轴于点B,且△AOB的面积为2$\sqrt{3}$,
∴S△AOB=$\frac{1}{2}$•OB•AB=$\frac{1}{2}$×$\sqrt{3}$•m=2$\sqrt{3}$,
∴m=4,A(-$\sqrt{3}$,4)
∴k=-$\sqrt{3}$m=-4$\sqrt{3}$;
(2)分类讨论:
①C点在负半轴.在△ABC中,AB=4,∠C=30°,
∴BC=4$\sqrt{3}$,C(-5$\sqrt{3}$,0);
解方程组$\left\{\begin{array}{l}{-5\sqrt{3}a+b=0}\\{-\sqrt{3}a+b=4}\end{array}\right.$得$\left\{\begin{array}{l}{a=\frac{\sqrt{3}}{3}}\\{b=5}\end{array}\right.$,
所以直线解析式为y=$\frac{\sqrt{3}}{3}$x+5.
②C点在正半轴.在△ABC中,AB=4,∠C=30°,
∴BC=4$\sqrt{3}$,C(3$\sqrt{3}$,0);
解方程组$\left\{\begin{array}{l}{3\sqrt{3}a+b=0}\\{-\sqrt{3}a+b=4}\end{array}\right.$得,$\left\{\begin{array}{l}{a=-\frac{\sqrt{3}}{3}}\\{b=3}\end{array}\right.$,
所以满足条件的直线解析式为y=-$\frac{\sqrt{3}}{3}$x+3.
综上所述,所以满足条件的直线解析式为y=$\frac{\sqrt{3}}{3}$x+5和y=-$\frac{\sqrt{3}}{3}$x+3.
点评 本题考查了一次函数和反比例函数的交点问题,此题中C点位置没有明确,需根据题意分情况探索,所以需分类讨论.分类讨论的思想训练学生思维的严密性.

 课课练江苏系列答案
课课练江苏系列答案 名牌中学课时作业系列答案
名牌中学课时作业系列答案 明天教育课时特训系列答案
明天教育课时特训系列答案 浙江新课程三维目标测评课时特训系列答案
浙江新课程三维目标测评课时特训系列答案| A. | 乙>甲>丙 | B. | 乙>丙>甲 | C. | 甲>乙>丙 | D. | 甲>丙>乙 |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
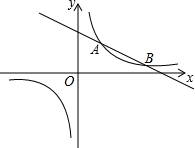 如图,一次函数,一次函数y=kx+5(k为常数,k≠0)的图象与反比例函数$y=\frac{8}{x}$的图象相交于A(2,b),B两点.
如图,一次函数,一次函数y=kx+5(k为常数,k≠0)的图象与反比例函数$y=\frac{8}{x}$的图象相交于A(2,b),B两点.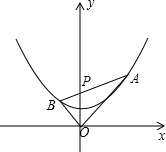 已知点P坐标为(0,2),点A是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的一个动点,直线AP与抛物线的另一个交点为点B,连结AO,BO.
已知点P坐标为(0,2),点A是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的一个动点,直线AP与抛物线的另一个交点为点B,连结AO,BO.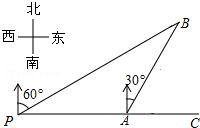 如图,某船从观测站P以每小时4海里的速度航行1小时到达港口A,再沿北偏东30°方向航行一段距离后到达港口B处,此时从观测点P处测得该船位于北偏东60°的方向,求港口B与观测站P之间的距离.
如图,某船从观测站P以每小时4海里的速度航行1小时到达港口A,再沿北偏东30°方向航行一段距离后到达港口B处,此时从观测点P处测得该船位于北偏东60°的方向,求港口B与观测站P之间的距离.