题目内容
5．
长方形ABCD中，∠ADB=20°，现将这一长方形纸片沿AF折叠，若使AB′∥BD，则折痕AF与AB的夹角∠BAF应为55°．
分析 先根据直角三角形的性质求出∠ABD的度数，再由平行线的性质求出∠BAB′的度数，根据图形翻折变换的性质即可得出结论．
解答 解：∵四边形ABCD是矩形，∠ADB=20°，
∴∠ABD=70°．
∵AB′∥BD，
∴∠BAB′=110°．
∵△AB′F由△ABF翻折而成，
∴∠BAF=$\frac{1}{2}$∠BAB′=55°．
故答案为：55°．
点评 本题考查的是平行线的性质，用到的知识点为：两直线平行，同旁内角互补．
练习册系列答案
浙江名校名师金卷系列答案
全优冲刺100分系列答案
相关题目
15．
如图，AB∥CD，直线EF与AB，CD相截，若∠5=62°，则∠4的度数是（ ）
如图，AB∥CD，直线EF与AB，CD相截，若∠5=62°，则∠4的度数是（ ）| A． | 28° | B． | 62° | C． | 118° | D． | 146° |
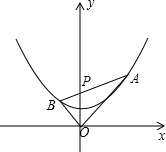已知点P坐标为（0，2），点A是抛物线y=$\frac{1}{4}$x2+1上在第一象限内的一个动点，直线AP与抛物线的另一个交点为点B，连结AO，BO．
20．点P（2，-7）位于（ ）
| A． | 第一象限 | B． | 第二象限 | C． | 第三象限 | D． | 第四象限 |