题目内容
2.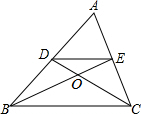 如图,在△ABC中,中线BE,CD相交于点O,连线DE,下列结论:
如图,在△ABC中,中线BE,CD相交于点O,连线DE,下列结论:①$\frac{DE}{BC}=\frac{1}{2}$;
$②\frac{{S}_{△ADE}}{{S}_{△ABC}}=\frac{1}{2}$;
③$\frac{AD}{AB}=\frac{OE}{OB}$;
④$\frac{{S}_{△ODE}}{{S}_{△DEC}}=\frac{1}{4}$
其中正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
分析 根据三角形的重心的概念和性质、相似三角形的性质计算即可.
解答 解:∵BE、CD是△ABC的中线,
∴DE是△ABC的中位线,
∴$\frac{DE}{BC}=\frac{1}{2}$,①正确;
$\frac{{S}_{△ADE}}{{S}_{△ABC}}$=$\frac{1}{4}$,②错误;
∵D是AB的中点,
∴$\frac{AD}{AB}$=$\frac{1}{2}$,
由题意得,点O是△ABC的重心,
∴$\frac{OE}{OB}$=$\frac{1}{2}$,
∴$\frac{AD}{AB}=\frac{OE}{OB}$,③正确;
$\frac{{S}_{△ODE}}{{S}_{△DEC}}$=$\frac{1}{3}$,④错误,
故选:B.
点评 本题考查的是三角形的重心的概念和性质、相似三角形的性质,掌握三角形的重心是三角形三条中线的交点,且重心到顶点的距离是它到对边中点的距离的2倍是解题的关键.

练习册系列答案
相关题目
10.将多项式-6a3b2-3a2b2因式分解时,应提取的公因式是( )
| A. | -3a2b2 | B. | -3ab | C. | -3a2b | D. | -3a3b3 |
12.比-2小1的数是( )
| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
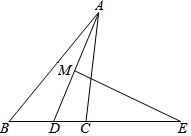 如图,已知在△ABC中,AD平分∠BAC,EM是AD的中垂线,交BC延长线于E.
如图,已知在△ABC中,AD平分∠BAC,EM是AD的中垂线,交BC延长线于E.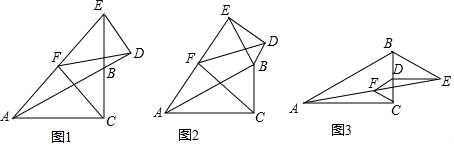
 如图所示,墙MN长为12m,要利用这面墙围一个矩形小院,面积为60m2,现有建材能建围墙总长至多26m,设AB=x m,BC=y m.
如图所示,墙MN长为12m,要利用这面墙围一个矩形小院,面积为60m2,现有建材能建围墙总长至多26m,设AB=x m,BC=y m.