题目内容
14.阅读下列文字:我们知道,对于一个图形,通过两种不同的方法计算它的面积,可以得到一个数学等式.例如由图1可以得到(a+2b)(a+b)=a2+3ab+2b2.
请解答下列问题:
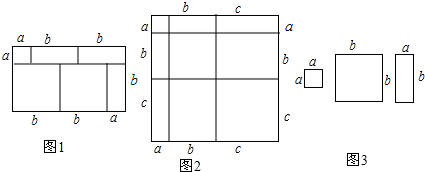
(1)写出图2中所表示的数学等式;
(2)利用(1)中所得到的结论,解决下面的问题:已知a+b+c=12,ab+bc+ac=42,求a2+b2+c2的值;
(3)图3中给出了若干个边长为a和边长为b的小正方形纸片及若干个边长分别为a、b的长方形纸片,请利用所给的纸片拼出一个几何图形,使得用两种不同的方法计算它的面积时,能够得到数学公式:2a2+7ab+3b2=(a+3b)(2a+b).
分析 (1)直接求得正方形的面积,然后再根据正方形的面积=各矩形的面积之和求解即可;
(2)将a+b+c=12,ab+bc+ac=42代入(1)中得到的关系式,然后进行计算即可;
(3)根据分解结果画出图形即可.
解答 解:(1)正方形的面积可表示为=(a+b+c)2;
正方形的面积=各个矩形的面积之和=a2+b2+c2+2ab+2bc+2ca,
所以(a+b+c)2=a2+b2+c2+2ab+2bc+2ca;
(2)∵a+b+c=12,ab+bc+ac=42,
∴由(1)可知:a2+b2+c2=(a+b+c)2-2(ab+bc+ca)=122-42×2=60;
(3)如图所示: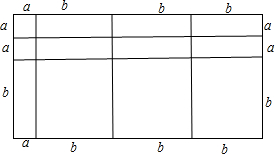
2a2+7ab+3b2=(a+3b)(2a+b).
点评 本题考查的是多项式乘多项式、因式分解的应用,利用面积法列出等式是解题的关键.

练习册系列答案
相关题目
6. 如图,扇形OMN的半径为3,弧$\widehat{MN}$=6,则扇形的面积是( )
如图,扇形OMN的半径为3,弧$\widehat{MN}$=6,则扇形的面积是( )
 如图,扇形OMN的半径为3,弧$\widehat{MN}$=6,则扇形的面积是( )
如图,扇形OMN的半径为3,弧$\widehat{MN}$=6,则扇形的面积是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
4.关于x的一元二次方程x2-x-(m+1)=0有两个不相等的实数根,则满足条件的m的最小整数为( )
| A. | -1 | B. | 0 | C. | 1 | D. | 2 |
 如图,直线y=2x+3与x轴交于点A,与y轴交于点B,D是射线AB上的动点(不与点A重合),DN⊥x轴于N,把△AND沿直线AB翻折,得到△AMD,延长MA交y轴于点C,过A、C、D三点的圆E与x轴交于点F,连结DF.
如图,直线y=2x+3与x轴交于点A,与y轴交于点B,D是射线AB上的动点(不与点A重合),DN⊥x轴于N,把△AND沿直线AB翻折,得到△AMD,延长MA交y轴于点C,过A、C、D三点的圆E与x轴交于点F,连结DF. 如图,在△ABC中,中线BE,CD相交于点O,连线DE,下列结论:
如图,在△ABC中,中线BE,CD相交于点O,连线DE,下列结论: 如图,菱形ABCD的边长是4cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为8$\sqrt{3}$cm2.
如图,菱形ABCD的边长是4cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为8$\sqrt{3}$cm2.