题目内容
11. 如图所示,墙MN长为12m,要利用这面墙围一个矩形小院,面积为60m2,现有建材能建围墙总长至多26m,设AB=x m,BC=y m.
如图所示,墙MN长为12m,要利用这面墙围一个矩形小院,面积为60m2,现有建材能建围墙总长至多26m,设AB=x m,BC=y m.(1)写出y与x之间的函数关系式;
(2)要求x和y都取整数,且小院的长宽比尽可能的小,x应取何值?
分析 (1)利用矩形的面积公式即可写出函数解析式;
(2)根据AB+BC+CD≤26,且x和y都是正整数即可求得x的值.
解答 解:(1)y=$\frac{60}{x}$;
(2)∵y=$\frac{60}{x}$,x,y都是整数,且2x+y≤26,且0<y≤12.
∴$\frac{120}{y}$+y≤26,且0<y≤12,
∴y的值只能取6,10,12.则对应的x的值依次是10,6,4.
则符合条件的建设方案只有BC=6cm,AB=10cm;BC=10cm,AB=6cm;BC=12cm,DC=5cm.
∵$\frac{6}{10}$<$\frac{10}{6}$<$\frac{12}{5}$,
∴x=10.
点评 本题考查了反比例函数的应用,正确根据条件确定y的值是关键.

练习册系列答案
相关题目
6. 如图,扇形OMN的半径为3,弧$\widehat{MN}$=6,则扇形的面积是( )
如图,扇形OMN的半径为3,弧$\widehat{MN}$=6,则扇形的面积是( )
 如图,扇形OMN的半径为3,弧$\widehat{MN}$=6,则扇形的面积是( )
如图,扇形OMN的半径为3,弧$\widehat{MN}$=6,则扇形的面积是( )| A. | 6 | B. | 7 | C. | 8 | D. | 9 |
16. 在平面内直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2017B2017C2017D2017的边长是( )
在平面内直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2017B2017C2017D2017的边长是( )
 在平面内直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2017B2017C2017D2017的边长是( )
在平面内直角坐标系中,正方形A1B1C1D1、D1E1E2B2、A2B2C2D2、D2E3E4B3…按如图所示的方式放置,其中点B1在y轴上,点C1、E1、E2、C2、E3、E4、C3…在x轴上,已知正方形A1B1C1D1的边长为1,∠B1C1O=60°,B1C1∥B2C2∥B3C3…则正方形A2017B2017C2017D2017的边长是( )| A. | ($\frac{\sqrt{3}}{3}$)2016 | B. | ($\frac{\sqrt{3}}{3}$)2017 | C. | ($\frac{1}{2}$)2016 | D. | ($\frac{1}{2}$)2017 |
 如图是从棱长为4的正方体的一角,挖去一个棱长为2的小正方体得到的立体图形,其主视图是( )
如图是从棱长为4的正方体的一角,挖去一个棱长为2的小正方体得到的立体图形,其主视图是( )



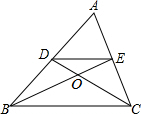 如图,在△ABC中,中线BE,CD相交于点O,连线DE,下列结论:
如图,在△ABC中,中线BE,CD相交于点O,连线DE,下列结论: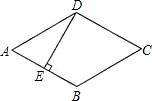 如图,菱形ABCD的边长是4cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为8$\sqrt{3}$cm2.
如图,菱形ABCD的边长是4cm,E是AB的中点,且DE⊥AB,则菱形ABCD的面积为8$\sqrt{3}$cm2.