题目内容
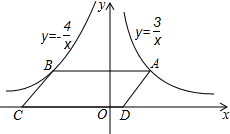 如图,点A是反比例函数y=
如图,点A是反比例函数y=| 3 |
| x |
| 4 |
| x |
| A、4 | B、5 | C、6 | D、7 |
考点:反比例函数系数k的几何意义,平行四边形的性质
专题:
分析:连结OA、OB,AB交y轴于E,由于AB⊥y轴,根据反比例函数y=
(k≠0)系数k的几何意义得到S△OEA=
×3=1.5,S△OBE=
×4=2,则四边形ABCD为平行四边形,然后根据平行四边形的性质得到S平行四边形ABCD=2S△OAB=7.
| k |
| x |
| 1 |
| 2 |
| 1 |
| 2 |
解答: 解:连结OA、OB,AB交y轴于E,如图,
解:连结OA、OB,AB交y轴于E,如图,
∵AB∥x轴,
∴AB⊥y轴,
∴S△OEA=
×3=1.5,S△OBE=
×4=2,
∴S△OAB=1.5+2=3.5,
∵四边形ABCD为平行四边形,
∴S平行四边形ABCD=2S△OAB=7.
故选:D.
 解:连结OA、OB,AB交y轴于E,如图,
解:连结OA、OB,AB交y轴于E,如图,∵AB∥x轴,
∴AB⊥y轴,
∴S△OEA=
| 1 |
| 2 |
| 1 |
| 2 |
∴S△OAB=1.5+2=3.5,
∵四边形ABCD为平行四边形,
∴S平行四边形ABCD=2S△OAB=7.
故选:D.
点评:本题考查了反比例函数y=
(k≠0)系数k的几何意义:从反比例函数y=
(k≠0)图象上任意一点向x轴和y轴作垂线,垂线与坐标轴所围成的矩形面积为|k|.
| k |
| x |
| k |
| x |

练习册系列答案
相关题目
 如图,BC=6,D、E分别是线段AB和线段AC的中点,那么线段DE的长是( )
如图,BC=6,D、E分别是线段AB和线段AC的中点,那么线段DE的长是( )| A、6 | B、5 | C、4.5 | D、3 |
已知a、b、c是三角形的三边长,如果满足(a-9)2+
+|c-15|=0,则三角形的形状是( )
| b-12 |
| A、底与腰不相等的等腰三角形 |
| B、等边三角形 |
| C、钝角三角形 |
| D、直角三角形 |
在?ABCD中,∠A:∠B:=2:3,则∠D=( )
| A、36° | B、108° |
| C、72° | D、60° |
若关于x的不等式组
有解,则m的取值范围是( )
|
| A、m<2 | B、m≤2 |
| C、m<-1 | D、-1≤m<2 |
 如图,△ABC中,AD=
如图,△ABC中,AD= 如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E.
如图,将矩形纸片ABCD沿其对角线AC折叠,使点B落在点B′的位置,AB′与CD交于点E.