题目内容
将一盒足量的牛奶按如图1所示倒入一个水平放置的长方体容器中,当容器中的牛奶刚好接触到点P时停止倒入.图2是它的平面示意图,请根据图中的信息,求出容器中牛奶的高度(结果精确到0.1cm).(参考数据:
≈1.73,
≈1.41)

| 3 |
| 2 |

考点:解直角三角形的应用
专题:几何图形问题
分析:根据题意得出AP,BP的长,再利用三角形面积求法得出NP的长,进而得出容器中牛奶的高度.
解答: 解:过点P作PN⊥AB于点N,
解:过点P作PN⊥AB于点N,
∵由题意可得:∠ABP=30°,AB=8cm,
∴AP=4cm,BP=AB•cos30°=4
cm,
∴NP×AB=AP×BP,
∴NP=
=
=2
(cm),
∴9-2
≈5.5(cm),
答:容器中牛奶的高度约为:5.5cm.
 解:过点P作PN⊥AB于点N,
解:过点P作PN⊥AB于点N,∵由题意可得:∠ABP=30°,AB=8cm,
∴AP=4cm,BP=AB•cos30°=4
| 3 |
∴NP×AB=AP×BP,
∴NP=
| AP×BP |
| AB |
4×4
| ||
| 8 |
| 3 |
∴9-2
| 3 |
答:容器中牛奶的高度约为:5.5cm.
点评:此题主要考查了解直角三角形以及三角形面积求法等知识,得出PN的长是解题关键.

练习册系列答案
相关题目
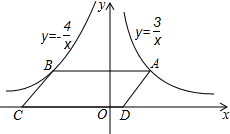 如图,点A是反比例函数y=
如图,点A是反比例函数y=

 如图是一个图案的一半,其中虚线是这个图案的对称轴,请你画出这个图案的另一半.
如图是一个图案的一半,其中虚线是这个图案的对称轴,请你画出这个图案的另一半. 如图,在长方形ABCD中,AB=18cm,CB=8cm.动点P从点A出发,以4cm/秒的速度由A-B-C-D运动,同时点Q从点B出发,以2cm/秒的速度由B-C-D运动,当P、Q中的某一点到达点D时同时停止运动.设运动时间为t秒.
如图,在长方形ABCD中,AB=18cm,CB=8cm.动点P从点A出发,以4cm/秒的速度由A-B-C-D运动,同时点Q从点B出发,以2cm/秒的速度由B-C-D运动,当P、Q中的某一点到达点D时同时停止运动.设运动时间为t秒.