题目内容
如图，△ABC中，AD=| 1 |
| 2 |
| 1 |
| 2 |
考点：三角形中位线定理
专题：
分析：根据已知条件推知DE是△ABC的中位线，利用三角形中位线定理得到BC=2DE．
解答：解：如图，∵△ABC中，AD=
AB，AE=
AC，
∴DE是△ABC的中位线，
∴BC=2DE．
又∵DE=6cm，
∴BC=12cm．
故答案是：12cm．
解：如图，∵△ABC中，AD=| 1 |
| 2 |
| 1 |
| 2 |
∴DE是△ABC的中位线，
∴BC=2DE．
又∵DE=6cm，
∴BC=12cm．
故答案是：12cm．
点评：此题考查的是三角形中位线的性质，即三角形的中位线平行于第三边且等于第三边的一半．
练习册系列答案
相关题目
观察函数的图象，回答以下问题：
如图，已知AB、CD相交于O，OE⊥CD于O，∠AOC=25°，则∠BOE的度数是（ ）| A、25° | B、65° |
| C、115° | D、130° |
若不等式组
的解集为x＞2013，则a的取值范围是（ ）
|
| A、a＞2013 |
| B、a＜2013 |
| C、a≥2013 |
| D、a≤2013 |
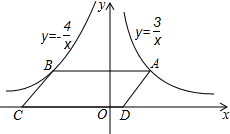如图，点A是反比例函数y=