题目内容
20.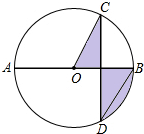 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )| A. | $\frac{2π}{3}$ | B. | π | C. | $\frac{π}{3}$ | D. | 2π |
分析 连接OD,则根据垂径定理可得出CE=DE,继而将阴影部分的面积转化为扇形OBD的面积,代入扇形的面积公式求解即可.
解答 解:连接OD,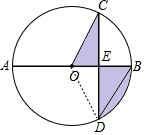
∵CD⊥AB,
∴CE=DE=$\frac{1}{2}$CD=$\sqrt{3}$(垂径定理),
故S△OCE=S△ODE,
即可得阴影部分的面积等于扇形OBD的面积,
又∵∠CDB=30°,
∴∠COB=60°(圆周角定理),
∴OC=2,
故S扇形OBD=$\frac{60π×{2}^{2}}{360}$=$\frac{2π}{3}$,
即阴影部分的面积为$\frac{2π}{3}$,
故选A.
点评 此题考查了扇形的面积计算、垂径定理及圆周角定理,解答本题关键是根据图形得出阴影部分的面积等于扇形OBD的面积,另外要熟记扇形的面积公式.

练习册系列答案
相关题目
8.已知一个角的余角是20°,则这个角的补角是( )
| A. | 70° | B. | 80° | C. | 110° | D. | 120° |
12.下列运算正确的是( )
| A. | 4m-m=3 | B. | 2a2-3a2=-a2 | C. | a2b-ab2=0 | D. | x-(y-x)=-y |
 如图所示,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=4cm,∠ABC=30°,则长方形纸条的宽度是2cm.
如图所示,将两张等宽的长方形纸条交叉叠放,重叠部分是一个四边形ABCD,若AD=4cm,∠ABC=30°,则长方形纸条的宽度是2cm.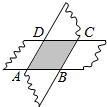 如图,剪两张对边平行的纸条,随意交又叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC什么关系?为什么?
如图,剪两张对边平行的纸条,随意交又叠放在一起,重合的部分构成了一个四边形,转动其中一张纸条,线段AD和BC什么关系?为什么?