题目内容
15.甲、乙两队进行乒乓球团体赛,比赛规划规定:两队之间进行2局比赛,3局比赛必须全部打完,只要赢满2局的队为获胜队,假设甲、乙两队之间每局比赛输赢的机会相同.(1)甲3局全胜的概率是$\frac{1}{8}$;
(2)如果甲队已经赢得了第1局比赛,那么甲队最终获胜的概率是多少?(请用“画树状图”或“列表”方法写出解答过程)
分析 (1)画树状图展示所有8种等可能的结果数,再找出甲3局全胜的结果数,然后根据概率公式求解;
(2)画树状图展示所有4种等可能的结果数,再找出甲队最终获胜的结果数,然后根据概率公式求解.
解答 解:(1)画树状图为:
共有8种等可能的结果数,其中甲3局全胜的结果数为1,
所以甲3局全胜的概率=$\frac{1}{8}$;
故答案为$\frac{1}{8}$;
(2)画树状图为:
共有4种等可能的结果数,其中甲队最终获胜的结果数为3,
所以甲队最终获胜的概率=$\frac{3}{4}$.
点评 本题考查了列表法与树状图法:利用列表法或树状图法展示所有等可能的结果n,再从中选出符合事件A或B的结果数目m,然后利用概率公式计算事件A或事件B的概率.

练习册系列答案
 新活力总动员暑系列答案
新活力总动员暑系列答案 龙人图书快乐假期暑假作业郑州大学出版社系列答案
龙人图书快乐假期暑假作业郑州大学出版社系列答案
相关题目
5.关于x的方程2x+4=3m和x-1=m有相同的解,则m的值是( )
| A. | 6 | B. | 5 | C. | $\frac{5}{2}$ | D. | -$\frac{2}{3}$ |
6.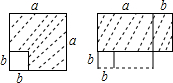 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )
 如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )
如图,在边长为a的正方形中挖掉一个边长为b的小正方形(a>b),把余下的部分剪拼成为一个矩形,通过计算两个图形(阴影部分)的面积,可以验证的等式是( )| A. | (a+2b)(a-b)=a2+ab-2b2 | B. | (a+b)2=a2+2ab+b2 | ||
| C. | (a-b)2=a2-2ab+b2 | D. | a2-b2=(a+b)(a-b) |
3. 如图,在△ABC中,DE∥BC,若AD=5,BD=10.AE=3,则CE=( )
如图,在△ABC中,DE∥BC,若AD=5,BD=10.AE=3,则CE=( )
 如图,在△ABC中,DE∥BC,若AD=5,BD=10.AE=3,则CE=( )
如图,在△ABC中,DE∥BC,若AD=5,BD=10.AE=3,则CE=( )| A. | 3 | B. | 6 | C. | 9 | D. | 12 |
10.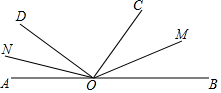 如图,点O在直线AB上,射线OC、OD在直线AB的同侧,∠AOD=40°,∠BOC=50°,OM、ON分别平分∠BOC和∠AOD,则∠MON的度数为( )
如图,点O在直线AB上,射线OC、OD在直线AB的同侧,∠AOD=40°,∠BOC=50°,OM、ON分别平分∠BOC和∠AOD,则∠MON的度数为( )
 如图,点O在直线AB上,射线OC、OD在直线AB的同侧,∠AOD=40°,∠BOC=50°,OM、ON分别平分∠BOC和∠AOD,则∠MON的度数为( )
如图,点O在直线AB上,射线OC、OD在直线AB的同侧,∠AOD=40°,∠BOC=50°,OM、ON分别平分∠BOC和∠AOD,则∠MON的度数为( )| A. | 135° | B. | 140° | C. | 152° | D. | 45° |
20.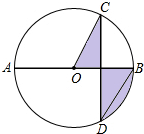 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
 如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )
如图,AB是⊙O的直径,弦CD⊥AB,∠CDB=30°,CD=2$\sqrt{3}$,则阴影部分的面积为( )| A. | $\frac{2π}{3}$ | B. | π | C. | $\frac{π}{3}$ | D. | 2π |
4.下列说法不正确的是( )
| A. | 1的平方根是±1 | B. | -1的立方根是-1 | ||
| C. | $\sqrt{16}$的算术平方根是2 | D. | $\sqrt{8}$是最简二次根式 |