题目内容
已知函数y=x2+mx+2,当1≤x≤2时,y>0恒成立,则m的取值范围为 .
考点:二次函数的性质
专题:计算题
分析:由于1≤x≤2时,y>0,则1+m+2>0和4+2m+2>0,解得m>-3,而y>0恒成立,所以抛物线在x轴上方,则△<0,即m2-8<0,解得m>-2
或m<2
,
然后确定m的取值范围.
| 2 |
| 2 |
然后确定m的取值范围.
解答:解:根据题意得x=1时,y=1+m+2>0,解得m>-3;
当x=2时,y=4+2m+2>0,解得m>-3,
△<0,即m2-8<0,解得m>-2
或m<2
,
所以m的取值范围为m>-2
.
故答案为m>-2
.
当x=2时,y=4+2m+2>0,解得m>-3,
△<0,即m2-8<0,解得m>-2
| 2 |
| 2 |
所以m的取值范围为m>-2
| 2 |
故答案为m>-2
| 2 |
点评:本题考查了二次函数的性质:二次函数y=ax2+bx+c(a≠0)的顶点坐标是(-
,
),对称轴直线x=-
,二次函数y=ax2+bx+c(a≠0)的图象具有如下性质:①当a>0时,抛物线y=ax2+bx+c(a≠0)的开口向上,当x<-
时,y随x的增大而减小;x>-
时,y随x的增大而增大;x=-
时,y取得最小值
,即顶点是抛物线的最低点.②当a<0时,抛物线y=ax2+bx+c(a≠0)的开口向下,x<-
,y随x的增大而增大;x>-
时,y随x的增大而减小;当x=-
时,y取得最大值
,即顶点是抛物线的最高点.
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |
| b |
| 2a |
| b |
| 2a |
| b |
| 2a |
| 4ac-b2 |
| 4a |

练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案 综合自测系列答案
综合自测系列答案
相关题目
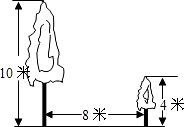 如图,有两棵树,一棵高10米,另一棵树高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )
如图,有两棵树,一棵高10米,另一棵树高4米,两树相距8米.一只鸟从一棵树的树梢飞到另一棵树的树梢,问小鸟至少飞行( )| A、8米 | B、10米 |
| C、12米 | D、14米 |
 已知抛物线对应的二次函数为y=a(x+10)(x+5),它与x轴交于A、B两点(A在B的左侧),与y轴交于C点,点D是以B为圆心、5为半径的圆周上位于第二象限内的动点,直线AD与y轴交于点E,设E(0,2t).
已知抛物线对应的二次函数为y=a(x+10)(x+5),它与x轴交于A、B两点(A在B的左侧),与y轴交于C点,点D是以B为圆心、5为半径的圆周上位于第二象限内的动点,直线AD与y轴交于点E,设E(0,2t).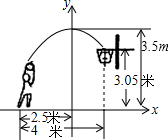 如图,一位篮球运动员甲在距篮球筐下4米处跳起投篮,球的运行线路为抛物线,当球运行到水平距离为2.5米时达到最高高度为3.5米,然后准确地落入篮筐,已知篮圈中心到地面的高度为3.05米,该运动员的身高为1.8米.
如图,一位篮球运动员甲在距篮球筐下4米处跳起投篮,球的运行线路为抛物线,当球运行到水平距离为2.5米时达到最高高度为3.5米,然后准确地落入篮筐,已知篮圈中心到地面的高度为3.05米,该运动员的身高为1.8米. 如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是
如图,⊙O的直径为10,圆心O到弦AB的距离OM的长为3,则弦AB的长是 如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为
如图,把矩形OABC放在直角坐标系中,OC在x轴上,OA在y轴上,且OC=2,OA=4,把矩形OABC绕着原点顺时针旋转90°得到矩形ODEF,则E的坐标为 如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.
如图,已知正方形ABCD,点E是BC上一点,点F是CD延长线上一点,连接EF,若BE=DF,点P是EF的中点.