题目内容
如图，⊙O的直径为10，圆心O到弦AB的距离OM的长为3，则弦AB的长是考点：垂径定理,勾股定理
专题：
分析：连接OA，先根据垂径定理求出AM=
AB，再根据勾股定理求出AM的值．
| 1 |
| 2 |
解答：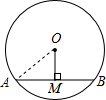
解：连接OA，
∵⊙O的直径为10，
∴OA=5，
∵圆心O到弦AB的距离OM的长为3，
由垂径定理知，点M是AB的中点，AM=
AB，
由勾股定理可得，AM=4，所以AB=8．
故答案为8．
解：连接OA，∵⊙O的直径为10，
∴OA=5，
∵圆心O到弦AB的距离OM的长为3，
由垂径定理知，点M是AB的中点，AM=
| 1 |
| 2 |
由勾股定理可得，AM=4，所以AB=8．
故答案为8．
点评：本题考查了垂径定理和勾股定理，通过连接OA构造直角三角形进而利用勾股定理求解．
练习册系列答案
相关题目
一次函数的图象过点（1，3）和（3，-1），且与x轴、y轴交于A、B两点．
如图，△ABC的外角∠DAC的平分线与内角∠ABC的平分线交于点E．若∠C=60°，求∠E．
如图，△DEF是由△ABC经过平移得到的，若∠C=80°，∠E=53°，则∠F=
如图，△ABO中，AB⊥OB，OB=下列运算正确的是（ ）
| A、2x+3y=5xy |
| B、（a-b）2=a2-b2 |
| C、5m2•m3=5m5 |
| D、m2•m3=m6 |
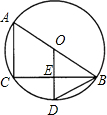如图，AB是⊙O的直径，BC是弦，OD⊥BC于E，交⊙O于点D．