Question

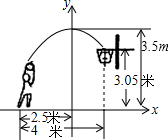如图，一位篮球运动员甲在距篮球筐下4米处跳起投篮，球的运行线路为抛物线，当球运行到水平距离为2.5米时达到最高高度为3.5米，然后准确地落入篮筐，已知篮圈中心到地面的高度为3.05米，该运动员的身高为1.8米．
（1）在这次投篮中，球在该运动员的头顶上方0.25米处出手，则当球出手时，该运动员离地面的高度为

 

米．
（2）运动员乙跳离地面时，最高能摸到3.3米运动员乙在运动员甲与篮板之间的什么范围内能在空中截住球？

Answer 1

考点：二次函数的应用

专题：

分析：（1）求出二次函数解析式，把相应的x的值代入抛物线解析式，求得球出手时的高度，减去0.25和运动员的身高即为该运动员离地面的高度；
（2）当y=3.3m，进而代入函数解析式，求出x的值，即可得出答案．

解答：解：（1）设抛物线的解析式为y=ax²+3.5，
∵（1.5，3.05）在抛物线上，
∴3.05=a×1.5²+3.5，
解得a=-0.2，
∴y=-0.2x²+3.5；
当x=-2.5时，y=2.25，
∴运动员离地面的高度为2.25-0.25-1.8=0.2（m），
故答案为0.2．

（2）由题意可得出：y=3.3，
则3.3=-0.2x²+3.5
解得：x₁=1，x₂=-1，
∴4-1=3（m），
∴乙在运动员甲与篮板之间的距离甲3米范围内能在空中截住球．

点评：此题主要考查了二次函数的应用；建立合适的平面直角坐标系是解决本题的突破点；求得球出手时距离地面的高度是解决本题的关键．