题目内容
 已知抛物线对应的二次函数为y=a(x+10)(x+5),它与x轴交于A、B两点(A在B的左侧),与y轴交于C点,点D是以B为圆心、5为半径的圆周上位于第二象限内的动点,直线AD与y轴交于点E,设E(0,2t).
已知抛物线对应的二次函数为y=a(x+10)(x+5),它与x轴交于A、B两点(A在B的左侧),与y轴交于C点,点D是以B为圆心、5为半径的圆周上位于第二象限内的动点,直线AD与y轴交于点E,设E(0,2t).(1)在抛物线对称轴上分别求满足下列条件的点的坐标(用t表示):
①求点P使APBE的周长最小:
②求点Q使QE-QB的值最大;
(2)若直线与CD与⊙B相切,试用t表示a;
(3)在(1)、(2)的条件下,若6≤OD≤8,求ACPB面积的取值范围.
考点:二次函数综合题
专题:
分析:(1)求出对称轴,根据①BE定值,故当P为直线AE与抛物线对称轴交点时,△PBE的周长最小,求出P点坐标;②当点Q位于直线EB与抛物线对称交点时,QE-QB的值最大,据此求出Q点坐标.
(2)若直线CD与⊙B相切,∠EAO=α,则∠ADB=∠ODC=α,在Rt△AOE中,易求得∠DEO=∠EDC=90°-α,∠DOE=α,故有CE=CD=OC,即是OE中点,判断出关系式;
(3)设抛物线对称轴与x轴交与T,则S△CPB=S梯形OCPT-S△CPB-S△COB,列出面积的表达式
t,根据t的取值范围求出面积的取值范围.
(2)若直线CD与⊙B相切,∠EAO=α,则∠ADB=∠ODC=α,在Rt△AOE中,易求得∠DEO=∠EDC=90°-α,∠DOE=α,故有CE=CD=OC,即是OE中点,判断出关系式;
(3)设抛物线对称轴与x轴交与T,则S△CPB=S梯形OCPT-S△CPB-S△COB,列出面积的表达式
| 5 |
| 2 |
解答: 解:(1)当y=0时,a(x+10)(x+5)=0,x1=-10,x2=-5.
解:(1)当y=0时,a(x+10)(x+5)=0,x1=-10,x2=-5.
对称轴为x=
=-7.5;
①如图a,∵点B和点A关于抛物线对称轴对称,而对于每一个确定的t值,BE定值,故当P为直线AE与抛物线对称轴交点时,△PBE的周长最小.
易求得直线EA对应的一次函数为:y=
x+2t,当x=-7.5时,y=0.5t,即P(-7.5,0.5t).
②如图b,当点Q位于直线EB与抛物线对称交点时,QE-QB的值最大,否则Q、B、E三点构成三角形,则QE-QB<EB,
由直线EB对应一次函数为:y=
x+2t,当x=-7.5时,y=-t,即Q(-7.5,-t);
 (2)如图c,令y=a(x+10)(x+5)中,x=0,得C(0,50a),
(2)如图c,令y=a(x+10)(x+5)中,x=0,得C(0,50a),
解法1:若直线CD与⊙B相切,连接BD,则BD⊥DC,又AO是⊙B的直径,
∴AD⊥DO,若设∠EAO=α,则∠ADB=∠ODC=α,在Rt△AOE中,
易求得∠DEO=∠EDC=90°-α,
∠DOE=α,故有CE=CD=OC,即是OE中点,故100a=2t,即t=50a.
解法2:∵CD、CO都与⊙B相切,
∴CD=CO,
∴∠CDO=∠COD,
在Rt△EDO中,∠DEO+∠DOE=90°,∠EDC+∠ODC=90°,
∴∠EDC=∠OEDC,
∴CD=CE,又由CD=CO,
∴CE=CO,即C是OE中点,
故100a=2t,即t=50a.
(3)解法1:易证Rt△OAD∽Rt△EAO,设OD=x,即
=
,即x2=
,由36≤
≤64,得
≤t≤
.
由(1)P(-7.5,0.5t),由(2)C(0,t),如图d,设抛物线对称轴与x轴交与T,则S△CPB=S梯形OCPT-S△CPB-S△COB=
(0.5t+t)×
-
×
×0.5t-
×5×t=
t,
∵
≤
t≤
,
 ∴△CPB的面积的取值范围是:
∴△CPB的面积的取值范围是:
≤S△CPB≤
.
解法2:由图e,当OD最长时,在Rt△AOD中,tan∠DAO=
=
,
在Rt△AOE中,tan∠EAO=
=
=
,即t=
,
同理,当OD最短时,t=
,故
≤t≤
,
如图e(为了清晰,隐藏了抛物线),
∵AE∥BC,
∴S△PBC=S△DBC,
又∵S△OBC=S△DBC,
∴S△PBC=S△OBC=
,
∵
≤
t≤
,
∴△CPB的面积的取值范围是:
≤S△CPB≤
.
 解:(1)当y=0时,a(x+10)(x+5)=0,x1=-10,x2=-5.
解:(1)当y=0时,a(x+10)(x+5)=0,x1=-10,x2=-5.对称轴为x=
| -10-5 |
| 2 |
①如图a,∵点B和点A关于抛物线对称轴对称,而对于每一个确定的t值,BE定值,故当P为直线AE与抛物线对称轴交点时,△PBE的周长最小.
易求得直线EA对应的一次函数为:y=
| t |
| 5 |
②如图b,当点Q位于直线EB与抛物线对称交点时,QE-QB的值最大,否则Q、B、E三点构成三角形,则QE-QB<EB,
由直线EB对应一次函数为:y=
| 2t |
| 5 |
 (2)如图c,令y=a(x+10)(x+5)中,x=0,得C(0,50a),
(2)如图c,令y=a(x+10)(x+5)中,x=0,得C(0,50a),解法1:若直线CD与⊙B相切,连接BD,则BD⊥DC,又AO是⊙B的直径,
∴AD⊥DO,若设∠EAO=α,则∠ADB=∠ODC=α,在Rt△AOE中,
易求得∠DEO=∠EDC=90°-α,
∠DOE=α,故有CE=CD=OC,即是OE中点,故100a=2t,即t=50a.
解法2:∵CD、CO都与⊙B相切,
∴CD=CO,
∴∠CDO=∠COD,
在Rt△EDO中,∠DEO+∠DOE=90°,∠EDC+∠ODC=90°,
∴∠EDC=∠OEDC,
∴CD=CE,又由CD=CO,
∴CE=CO,即C是OE中点,
故100a=2t,即t=50a.
(3)解法1:易证Rt△OAD∽Rt△EAO,设OD=x,即
| x |
| 2t |
| 10 | ||
|
| 100t2 |
| 25+t2 |
| 100t2 |
| 25+t2 |
| 15 |
| 4 |
| 20 |
| 3 |
由(1)P(-7.5,0.5t),由(2)C(0,t),如图d,设抛物线对称轴与x轴交与T,则S△CPB=S梯形OCPT-S△CPB-S△COB=
| 1 |
| 2 |
| 15 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
| 1 |
| 2 |
| 5 |
| 2 |
∵
| 75 |
| 8 |
| 5 |
| 2 |
| 50 |
| 3 |
 ∴△CPB的面积的取值范围是:
∴△CPB的面积的取值范围是:| 75 |
| 8 |
| 50 |
| 3 |
解法2:由图e,当OD最长时,在Rt△AOD中,tan∠DAO=
| OD |
| OA |
| 4 |
| 3 |
在Rt△AOE中,tan∠EAO=
| OE |
| AO |
| 2t |
| 10 |
| 4 |
| 3 |
| 20 |
| 3 |
同理,当OD最短时,t=
| 15 |
| 4 |
| 15 |
| 4 |
| 20 |
| 3 |
如图e(为了清晰,隐藏了抛物线),
∵AE∥BC,
∴S△PBC=S△DBC,
又∵S△OBC=S△DBC,
∴S△PBC=S△OBC=
| 5t |
| 2 |
∵
| 75 |
| 8 |
| 5 |
| 2 |
| 50 |
| 3 |
∴△CPB的面积的取值范围是:
| 75 |
| 8 |
| 50 |
| 3 |
点评:本题考查了二次函数综合题,涉及相似三角形、圆等知识,要充分利用数形结合思想进行分析,找到解决问题的突破口.同时要注意一题多解,提升能力.

练习册系列答案
相关题目
 如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF;
如图,在正方形ABCD中,点P是AB上一动点(不与A、B重合),对角线AC、BD相交于点O,过点P分别作AC、BD的垂线,分别交AC、BD于点E、F,交AD、BC于点M、N.下列结论:①△APE≌△AME;②PM+PN=AC;③PE2+PF2=PO2;④△POF∽△BNF; 在矩形ABCD中,AB=4,BC=8,点E、F分别在边AD、BC上,BF=DE=3,求证:四边形AFCE是菱形.
在矩形ABCD中,AB=4,BC=8,点E、F分别在边AD、BC上,BF=DE=3,求证:四边形AFCE是菱形.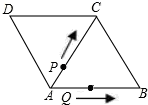 如图,菱形ABCD的边长为12cm,∠B=60°,从初始时刻开始,点P、Q同时从A点出发,点P以2cm/秒的速度沿A→C→B的方向运动,点Q以4cm/秒的速度沿A→B→C→D的方向运动,当Q点运动点D点时,P、Q两点同时停止运动.设P、Q运动的时间为x秒时,解答下列问题:
如图,菱形ABCD的边长为12cm,∠B=60°,从初始时刻开始,点P、Q同时从A点出发,点P以2cm/秒的速度沿A→C→B的方向运动,点Q以4cm/秒的速度沿A→B→C→D的方向运动,当Q点运动点D点时,P、Q两点同时停止运动.设P、Q运动的时间为x秒时,解答下列问题: 一次函数的图象过点(1,3)和(3,-1),且与x轴、y轴交于A、B两点.
一次函数的图象过点(1,3)和(3,-1),且与x轴、y轴交于A、B两点.
 全面实现低碳生活已逐渐成为人们的共识.某企业为了发展低碳经济,采用技术革新,减少二氧化碳的排放.随着排放量的减少,企业相应获得的利润也有所提高,且相应获得的利润y(万元)与月份x(月)
全面实现低碳生活已逐渐成为人们的共识.某企业为了发展低碳经济,采用技术革新,减少二氧化碳的排放.随着排放量的减少,企业相应获得的利润也有所提高,且相应获得的利润y(万元)与月份x(月)