题目内容
3.给出代数式n•(n+2)-(n+1)2.(1)当n的值为1,2,3,4,5时,分别求该代数式的值;
(2)根据(1)的计算结果,小康就猜想:当n为任意正整数时,n(n+2)-(n+1)2的值都是-1,你认为小康的猜想正确吗?请说说你的理由.
分析 (1)把n=1,2,3,4,5分别代入代数式求出值即可;
(2)小明的猜想正确,根据单项式乘以单项式,完全平方公式和合并同类项的计算法则计算即可求解.
解答 解:(1)当n=1时,原式=1×3-4=-1;
当n=2时,原式=2×4-9=-1;
当n=3时,原式=3×5-16=-1;
当n=4时,原式=4×6-25=-1;
当n=5时,原式=5×7-36=-1;
(2)小康的猜想正确,
n•(n+2)-(n+1)2
=n2+2n-n2-2n-1
=-1.
点评 此题考查了代数式求值,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
14.我市为实现“四城同创”目标,绿化办计划为某新开发住宅小区购买并种植400株树苗,某苗圃公司提供以下信息:
①可供选择的树苗有杨树、柳树和樟树三种,并且要求购买杨树、柳树的数量相等.
②如表:
设购买杨树、樟树的数量分别为x株、y株.
(1)写出y与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当每株樟树的批发价p等于3元时,要使这400棵树苗两年后对该住宅小区的空气净化指数不低于90,就怎样安排这三种树苗的购买数量,才能使购买树苗的总费用最低?最低总费用是多少?
(3)当每株樟树批发价p(元)与购买数量y(株)之间存在关系p=3-0.005y时,求购买树苗的总费用W(元)与购买杨树数量x(株)之间的函数关系式(不要求写出自变量的取值范围).
①可供选择的树苗有杨树、柳树和樟树三种,并且要求购买杨树、柳树的数量相等.
②如表:
| 树苗 | 每株树批发价格(元) | 两年后每株树苗对空气的净化指数 |
| 杨树 | 3 | 0.4 |
| 柳树 | 2 | 0.1 |
| 樟树 | p | 0.2 |
(1)写出y与x之间的函数关系式(不要求写出自变量的取值范围);
(2)当每株樟树的批发价p等于3元时,要使这400棵树苗两年后对该住宅小区的空气净化指数不低于90,就怎样安排这三种树苗的购买数量,才能使购买树苗的总费用最低?最低总费用是多少?
(3)当每株樟树批发价p(元)与购买数量y(株)之间存在关系p=3-0.005y时,求购买树苗的总费用W(元)与购买杨树数量x(株)之间的函数关系式(不要求写出自变量的取值范围).
 如图,△ABC中,∠ACB=90°,∠CAB=45°,E是BC边上任意一点,过点C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
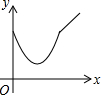
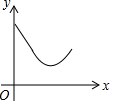
如图,△ABC中,∠ACB=90°,∠CAB=45°,E是BC边上任意一点,过点C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.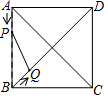 如图,正方形ABCD中,动点P的运动路线为AB→BC,动点Q的运动路线为对角线BD,点P,Q以同样的速度分别从A,B两点同时出发匀速前进,当一个点到达终点停止运动时,另一个点也随之停止.设点P的运动路程为x,PQ的长为y,则下列能大致表示y与x的函数关系的图象为( )
如图,正方形ABCD中,动点P的运动路线为AB→BC,动点Q的运动路线为对角线BD,点P,Q以同样的速度分别从A,B两点同时出发匀速前进,当一个点到达终点停止运动时,另一个点也随之停止.设点P的运动路程为x,PQ的长为y,则下列能大致表示y与x的函数关系的图象为( )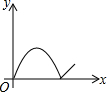

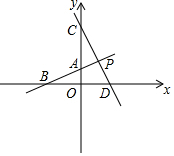 如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA:AC=2:5,直线CD垂直于直线AB于点P,交x轴于点D.
如图,直线AB与坐标轴分别交于点A、点B,且OA、OB的长分别为方程x2-6x+8=0的两个根(OA<OB),点C在y轴上,且OA:AC=2:5,直线CD垂直于直线AB于点P,交x轴于点D.