题目内容
8. 如图,△ABC中,∠ACB=90°,∠CAB=45°,E是BC边上任意一点,过点C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.
如图,△ABC中,∠ACB=90°,∠CAB=45°,E是BC边上任意一点,过点C作CF⊥AE,垂足为F,过B作BD⊥BC交CF的延长线于D.(1)求证:AE=CD.
(2)若AE是BC边上的中线,且AC=12cm,求BD的长.
分析 (1)根据同角的余角相等求出∠BCD=∠CAE,再求出△ABC是等腰直角三角形,根据等腰直角三角形的性质可得AC=BC,再利用全等三角形对应边相等证明即可;
(2)根据全等三角形对应边相等可得BD=CE,再根据线段中点的定义解答.
解答 (1)证明:∵∠ACB=90°,
∴∠BCD+∠ACD=90°,
∵CF⊥AE,
∴∠AFC=90°,
∴∠CAE+∠ACD=90°,
∴∠BCD=∠CAE,
∵∠ACB=90°,∠CAB=45°,
∴△ABC是等腰直角三角形,
∴AC=BC,
在△ACE和△CBD中,$\left\{\begin{array}{l}{∠BCD=∠CAE}\\{∠ACE=∠CBD=90°}\\{AC=BC}\end{array}\right.$,
∴△ACE≌△CBD(AAS),
∴AE=CD;
(2)解:∵△ACE≌△CBD,
∴BD=CE,
∵AE是BC边上的中线,且AC=12cm,
∴CE=$\frac{1}{2}$BC=$\frac{1}{2}$AC=$\frac{1}{2}$×12=6cm,
∴BD=6cm.
点评 本题考查了全等三角形的判定与性质,等腰直角三角形的判定与性质,熟练掌握三角形全等的判断方法是解题的关键.

练习册系列答案
相关题目
18.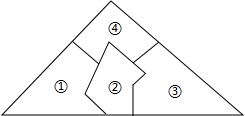 一块三角形玻璃被小明碰碎成四块(如图),为了配一块和以前一样的玻璃,小明只需带其中的两块去玻璃店即可,则他可以选择的是( )
一块三角形玻璃被小明碰碎成四块(如图),为了配一块和以前一样的玻璃,小明只需带其中的两块去玻璃店即可,则他可以选择的是( )
 一块三角形玻璃被小明碰碎成四块(如图),为了配一块和以前一样的玻璃,小明只需带其中的两块去玻璃店即可,则他可以选择的是( )
一块三角形玻璃被小明碰碎成四块(如图),为了配一块和以前一样的玻璃,小明只需带其中的两块去玻璃店即可,则他可以选择的是( )| A. | 带其中的任意两块 | B. | 带①和② | ||
| C. | 带①和③ | D. | 带③和④ |
19.下列图形中,既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |
 如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一直线上.
如图,△ABC和△ADE都是等腰三角形,且∠BAC=90°,∠DAE=90°,B,C,D在同一直线上. 如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG
如图,在△ABC中,∠ACB=90°,AC=BC,BE是中线,CG平分∠ACB交BE于点G,F为AB边上一点,且∠ACF=∠CBG
 如图在△ABC中,∠B=40°,∠C=60°,AD⊥BC于点D,AE平分∠BAC交BC于点E,DF⊥AE于点F.求∠ADF的度数.
如图在△ABC中,∠B=40°,∠C=60°,AD⊥BC于点D,AE平分∠BAC交BC于点E,DF⊥AE于点F.求∠ADF的度数.