题目内容
5.(1)计算:2cos45°-(-$\frac{1}{4}$)-1-$\sqrt{8}$-(π-$\sqrt{3}$)0.(2)化简并求值:$(1-\frac{{{a^2}+8}}{{{a^2}+4a+4}})÷\frac{4a-4}{{{a^2}+2a}}$,其中a=$\sqrt{3}$-1.
分析 (1)根据特殊角的三角函数值、负整数指数幂、二次根式的化简、0指数幂的定义解答;
(2)先将括号内的部分加减,因式分解后约分即可.
解答 解:(1)原式=2×$\frac{\sqrt{2}}{2}$-$\frac{1}{-\frac{1}{4}}$-2$\sqrt{2}$-1
=$\sqrt{2}$+4-2$\sqrt{2}$-1
=3-$\sqrt{2}$;
(2)原式=[1-$\frac{{a}^{2}+8}{(a+2)^{2}}$]•$\frac{a(a+2)}{4(a-1)}$
=$\frac{{a}^{2}+4a+4-{a}^{2}-8}{(a+2)^{2}}$
=$\frac{4a-4}{{(a+2)}^{2}}$•$\frac{a(a+2)}{4(a-1)}$
=$\frac{a}{a+2}$,
当a=$\sqrt{3}$-1时,原式=$\frac{\sqrt{3}-1}{\sqrt{3}-1+2}$
=$\frac{\sqrt{3}-1}{\sqrt{3}+1}$
=$\frac{3+1-2\sqrt{3}}{2}$
=2-$\sqrt{3}$.
点评 (1)本题考查了实数的运算,涉及特殊角的三角函数值、负整数指数幂、二次根式的化简、0指数幂等运算,属于基础题;
(2)本题考查了分式的化简求值,熟悉通分、约分因式分解是解题的关键.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案
相关题目
16.截至2014年1月初,济南户籍总人口613.4万人,其中613.4万人用科学记数法表示为( )
| A. | 6.134×102人 | B. | 613.4×104人 | C. | 6.134×105人 | D. | 6.134×106人 |
20.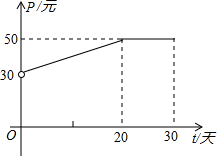 根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
(1)根据图象,写出该产品每件销售价格P与时间t的函数解析式;
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量.
 根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.
根据市场调查,某种新产品投放市场的30天内,每件销售价格P(元)与时间t(天)的关系如图所示,日销售量Q(件)与时间t(天)之间的关系如表所示.| t/天 | 5 | 15 | 20 | 30 |
| Q/件 | 35 | 25 | 20 | 10 |
(2)在所给的直角坐标系中,根据表中提供的数据描出实数对(t,Q)的对应点,并确定日销售量Q与时间t的一个函数解析式;
(3)在这30天内,哪一天的日销售金额最大?(日销售金额=每件产品销售价格×日销售量.
15.下列命题中,是真命题的有( )
| A. | 等角的余角角相等 | B. | 同位角相等 | ||
| C. | 若a2=b2,则a=b | D. | 相等角是对顶角 |
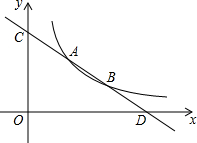 如图,点A(m,m+1),B(m+3,m-1)为第一象限内的点,并且都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,直线AB与y轴交于点C.
如图,点A(m,m+1),B(m+3,m-1)为第一象限内的点,并且都在反比例函数y=$\frac{k}{x}$(k≠0)的图象上,直线AB与y轴交于点C.
 小明家离学校1880米,其中有一段为上坡路,另一段为下坡路,如图所示,他骑自行车去上学用了10分钟.已知小明在上坡路上的平均速度是6千米/时,下坡路上的平均速度为12千米/时,问小明在上学路上走上坡路、下坡路各用了多少分钟?
小明家离学校1880米,其中有一段为上坡路,另一段为下坡路,如图所示,他骑自行车去上学用了10分钟.已知小明在上坡路上的平均速度是6千米/时,下坡路上的平均速度为12千米/时,问小明在上学路上走上坡路、下坡路各用了多少分钟?