题目内容
4.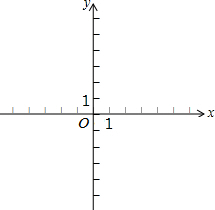 作出函数y1=2x-2与y2=-2x+6的图象,利用图象解答下列问题:
作出函数y1=2x-2与y2=-2x+6的图象,利用图象解答下列问题:(1)方程组$\left\{\begin{array}{l}2x-y=2\\ 2x+y=6\end{array}\right.$的解为$\left\{\begin{array}{l}{x=2}\\{y=2}\end{array}\right.$;
(2)y1>0与y2>0同时成立时x取何值范围是1<x<3;
(3)直线y1=2x-2的图象与y轴交于点A,直线y2=-2x+6的图象与y轴交于点B,两者相交于点C,求△ABC的三角形的面积;
(4)在直线y1=2x-2的图象上存在异于点C的另一点P,使得△ABC与△ABP的面积相等,请求出点P的坐标.
分析 (1)根据题意画出图象,利用其交点坐标得出方程组的解;
(2)利用函数图象得出在x轴上方时,对应x的取值范围;
(3)利用已知图象结合三角形面积求法得出答案;
(4)利用三角形面积求法得出P点横坐标,进而代入函数解析式得出P点坐标.
解答  解:(1)如图所示:方程组$\left\{\begin{array}{l}2x-y=2\\ 2x+y=6\end{array}\right.$的解为:$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$;
解:(1)如图所示:方程组$\left\{\begin{array}{l}2x-y=2\\ 2x+y=6\end{array}\right.$的解为:$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$;
故答案为:$\left\{\begin{array}{l}x=2\\ y=2\end{array}\right.$;
(2)如图所示:当y1>0与y2>0同时成立时,
x取何值范围是:1<x<3;
故答案为:1<x<3;
(3)∵x=0时,y1=6,
x=0,y2=-2,
则AB=8,
故△ABC的三角形的面积为:$\frac{1}{2}$×8×2=8;
(4)如图所示:当P点横坐标为:-2,△ABC与△ABP的面积相等,
故y1=2x-2=-6,
则P点坐标为:(-2,-6),
此时△ABC与△ABP的面积相等.
点评 此题主要考查了一次函数与二元一次方程组以及一次函数与一元一次不等式和三角形面积求法等知识,正确利用数形结合分析是解题关键.

练习册系列答案
相关题目
20.在梯形ABCD中,AD∥BC,BC=BD,AD=CD,且∠C=80°,则∠A=( )
| A. | 120° | B. | 130° | C. | 140° | D. | 150° |
13.气象台为了预报台风,首先要确定台风中心的位置,则下列说法能确定台风中心位置的是( )
| A. | 西太平洋 | B. | 距电白500海里 | C. | 北纬28°,东经36° | D. | 湛江附近 |

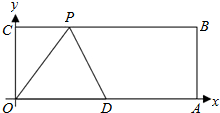 已知:如图,O为坐标原点,四边形OABC为长方形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是等腰三角形时.
已知:如图,O为坐标原点,四边形OABC为长方形,A(10,0),C(0,4),点D是OA的中点,点P在BC上运动,当△ODP是等腰三角形时.