题目内容
12. 如图,已知BD是Rt△ABC的腰AC上的中线,AE⊥BD,交BD于点E,延长AE交BC于点F,求证:∠ADB=∠CDF.
如图,已知BD是Rt△ABC的腰AC上的中线,AE⊥BD,交BD于点E,延长AE交BC于点F,求证:∠ADB=∠CDF.
分析 过A、D分别做BC的垂线,设AG的长为1,得出与之相关联的线段的长度,进而利用角的正切值相等得出∠DBH=∠FDH,即可得出结论.
解答 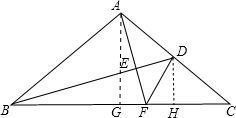 证明:过A、D分别做BC的垂线,垂足分别为G、H.
证明:过A、D分别做BC的垂线,垂足分别为G、H.
设AG=1,那么CG=1,DH=$\frac{1}{2}$,BH=$\frac{2}{3}$,
tan∠DBH=$\frac{1}{3}$,
又∵∠GAF=∠DBH,
∴GF=$\frac{1}{3}$AG=$\frac{1}{3}$,
FH=GH-GF=$\frac{1}{2}$-$\frac{1}{3}$=$\frac{1}{6}$,
tan∠FDH=$\frac{FH}{DH}$=$\frac{1}{3}$
∴∠DBH=∠FDH
∵∠ADB=∠DBH+∠C,
∠CDF=∠FDH+∠CDH,
∴∠ADB=∠CDF.
点评 本题主要考查了全等三角形的判定与性质,等腰三角形的性质以及由正切值判定两个角相等,无论是证明还是计算题,都应该从不同角度思考,利用已学知识熟练求解.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.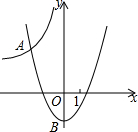 如图,二次函数y=x2+bx+c的图象过点B(0,-2),它与反比例函数y=-$\frac{8}{x}$的图象交于点A(m,4),则这二次函数图象的对称轴是( )
如图,二次函数y=x2+bx+c的图象过点B(0,-2),它与反比例函数y=-$\frac{8}{x}$的图象交于点A(m,4),则这二次函数图象的对称轴是( )
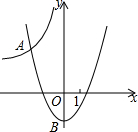 如图,二次函数y=x2+bx+c的图象过点B(0,-2),它与反比例函数y=-$\frac{8}{x}$的图象交于点A(m,4),则这二次函数图象的对称轴是( )
如图,二次函数y=x2+bx+c的图象过点B(0,-2),它与反比例函数y=-$\frac{8}{x}$的图象交于点A(m,4),则这二次函数图象的对称轴是( )| A. | 直线x=$\frac{1}{4}$ | B. | 直线x=$\frac{1}{3}$ | C. | 直线x=$\frac{1}{2}$ | D. | 直线x=$\frac{2}{3}$ |
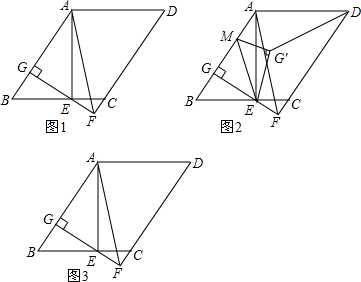
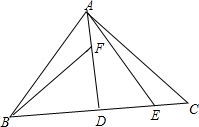 如图,在Rt△BAC中,已知AB=AC,∠BAC=90°,AD⊥BC于点D,点F、E分别在AD、DC上,且AF=CE,连接BF、AE.
如图,在Rt△BAC中,已知AB=AC,∠BAC=90°,AD⊥BC于点D,点F、E分别在AD、DC上,且AF=CE,连接BF、AE.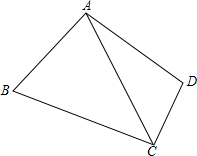 如图所示四边形ABCD,AB=AD,∠BAD=∠BCD=90°,SABCD=24cm2,求AC的长.
如图所示四边形ABCD,AB=AD,∠BAD=∠BCD=90°,SABCD=24cm2,求AC的长.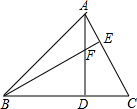 如图,在△ABC中,AD⊥BC,BE⊥AC,AD=BD,求证:BF=AC.
如图,在△ABC中,AD⊥BC,BE⊥AC,AD=BD,求证:BF=AC. 如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标(1.2),
如图,直角坐标系中,△ABC的顶点都在网格点上,其中C点坐标(1.2),