题目内容
20.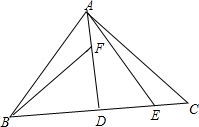 如图,在Rt△BAC中,已知AB=AC,∠BAC=90°,AD⊥BC于点D,点F、E分别在AD、DC上,且AF=CE,连接BF、AE.
如图,在Rt△BAC中,已知AB=AC,∠BAC=90°,AD⊥BC于点D,点F、E分别在AD、DC上,且AF=CE,连接BF、AE.(1)求证:△ABF≌△CAE;
(2)判断BF与AE具有怎样的位置关系?并说明理由.
分析 (1)由等腰直角三角形的性质得出∠C=45°,∠BAD=$\frac{1}{2}$∠BAC=45°,根据SAS即可证明△ABF≌△CAE;
(2)延长BF交AE于G,由△ABF≌△CAE,得出∠ABF=∠CAE,得出∠ABF+∠BAG=∠BAC=90°,因此∠AGB=90°,证出BG⊥AE即可.
解答 (1)证明:∵AB=AC,∠BAC=90°,AD⊥BC,
∴∠C=45°,∠BAD=$\frac{1}{2}$∠BAC=45°,
在△ABF和△CAE中,$\left\{\begin{array}{l}{AF=CE}&{\;}\\{∠BAF=∠C=45°}&{\;}\\{AB=CA}&{\;}\end{array}\right.$,
∴△ABF≌△CAE(SAS);
(2)解:BF⊥AE;理由如下:延长BF交AE于G,如图所示: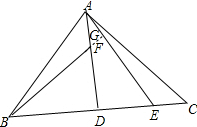 ∵△ABF≌△CAE,
∵△ABF≌△CAE,
∴∠ABF=∠CAE,
∵∠ABF+∠BAG=∠CAE+∠BAG=∠BAC=90°,
∴∠AGB=90°,
∴BG⊥AE,
∴BF⊥AE.
点评 本题考查了等腰直角三角形的性质、全等三角形的判定与性质以及垂线的判定方法;熟练掌握等腰直角三角形的性质,并能进行推理论证是解决问题的关键.

练习册系列答案
 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案
相关题目
11. 在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )
在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )
 在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )
在长为20m,宽为16m的长方形空地上,沿平行于长方形各边的方向割出三个完全相同的小长方形花圃,其示意图如图所示,则花圃的面积是( )| A. | 64m2 | B. | 32m2 | C. | 128m2 | D. | 96m2 |

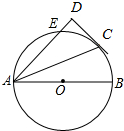 如图,AB是⊙O直径,Rt△ACD的直角边CD与⊙O相切,切点为C,直角边AD与⊙O相交于点E,∠BAC=22.5°,
如图,AB是⊙O直径,Rt△ACD的直角边CD与⊙O相切,切点为C,直角边AD与⊙O相交于点E,∠BAC=22.5°,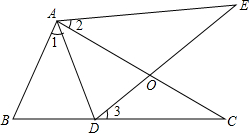 如图,∠1=∠2=∠3,AB=AD,请说明BC=DE.
如图,∠1=∠2=∠3,AB=AD,请说明BC=DE. 如图,已知BD是Rt△ABC的腰AC上的中线,AE⊥BD,交BD于点E,延长AE交BC于点F,求证:∠ADB=∠CDF.
如图,已知BD是Rt△ABC的腰AC上的中线,AE⊥BD,交BD于点E,延长AE交BC于点F,求证:∠ADB=∠CDF.